- Index
 ImageMagick Examples Preface and Index
ImageMagick Examples Preface and Index
 Solid Color Canvases
Solid Color Canvases
 (for image manipulations)
(for image manipulations)
 Gradients of Colors
Gradients of Colors
 (canvases of smooth color changes)
(canvases of smooth color changes)
 Sparse Points of Color
Sparse Points of Color
 (coloring from fixed points)
(coloring from fixed points)
 Randomized Canvases
Randomized Canvases
 (for randomized background images)
(for randomized background images)
 Tiled Canvases
Tiled Canvases
 (canvases using a repeating images)
(canvases using a repeating images)
Canvases are used by ImageMagick both as a starting image for drawing on,
backgrounds to overlay images with transparent areas, or even just as part of
general image processing. They can be a solid color, or a range of colors,
or even a tile of a smaller image. Here we look at some of the more common
methods of generating a canvas image.
Solid Color Canvases
Direct Generation
Generating a canvas of a specific color and size is very simple to do, and is
used all the time...
convert -size 100x100 xc:khaki canvas_khaki.gif
|
|
![[IM Output]](canvas_khaki.gif)
|
If you have already created a canvas, but need one in a different color you
can replace that color using the "-opaque" operator.
convert canvas_khaki.gif -fill tomato -opaque khaki canvas_opaque.gif
| |
![[IM Output]](canvas_opaque.gif)
|
You can even grab a single pixel from an existing image, and expand it to the
canvas size you want. We use "
-scale" for a simple and fast resizing of the single pixel.
Here we grab a rose color from the built-in "rose:" image.
convert rose: -crop 1x1+40+30 +repage -scale 100x100\! canvas_pick.gif
| |
![[IM Output]](canvas_pick.gif)
|
Create Image of same size
One most basic techniques when using ImageMagick is to generate a canvas the
same size as some existing image. This can be done by converting that
existing image into the canvas need, but preserving the images original size.
Naturally IM provides a large number of ways to do this, usually as a side
effect of other image operations. But only one method currently stands out
from the rest and is obvious in its intent.
|
To the left is a test image... Don't worry above how I actually generated this
image, it is not important for the exercise. I did design it to contain a
range of colors, transparencies and other features, specifically to give IM a
good workout when used.
If you are really interested in the commands used to generate this image
you can look at the special script, "generate_test", I use to create it.
|
![[IM Output]](test.png)
|
Overlay a Specific Color
The simplest way is to use "-colorize" to overlay the fill color but with a fully opaque
value. However this will preserve the original images alpha channel, unless
you remove it first, using "+matte".
convert test.png +matte -fill Sienna -colorize 100% color_colorize.gif
|
|
![[IM Output]](color_colorize.gif)
|
As of IM v6.4.2-1 you can also use the "+level-colors" to set all
the colors.
convert test.png -alpha Opaque +level-colors Chocolate color_levelc.gif
|
|
![[IM Output]](color_levelc.gif)
|
  |
Note that "+matte" is
equivelent to "-alpha Off" so the resulting image will not
have an active or working transparency channel. On the other hand using
"-alpha Opaque" will make the image fully
opaque, but will still contain an active transparency channel that you can
use it in later operations.
|
As of IM v6.4.3-0 you can use the "-sparse-color" operator to
set a single point to the color wanted, using just about any method it
provides (see Sparse Points of Color below).
convert test.png -alpha Off \
-sparse-color Voronoi '0,0 Peru' color_sparse.gif
|
|
![[IM Output]](color_sparse.gif)
|
A more general way people think of is to use "-draw" to reset all the colors in
the current image to the current "-fill" color.
convert test.png -fill Tan -draw 'color 0,0 reset' color_reset.gif
|
|
![[IM Output]](color_reset.gif)
|
All these methods will also preserve any meta-data the image may contain (such
as comments or profiles). This can be important if you want to annotate those
comments on the blank canvas, or you plan to overlay the original image onto
the canvas and want to keep that meta data intact.
There are a huge number of other methods as well but are usally regarded as
more complex as it involves using special
Alpha
Composition to force various operators to replace the image with the
desired color. This technique only works with image operators that use
"
-compose", to replace
the existing image, with the desired color.
If you are just wanting to grab the original images meta-data (such as its
commend an labels, but want a specific color and size of canvas image, the
"-extent" operator (See
Extent, Direct Image Size Adjustment) may be the
simplest. Color will again come from the "-background" setting.
convert test.png -background LemonChiffon \
-compose Dst -extent 100x100 color_extent.gif
|
|
![[IM Output]](color_extent.gif)
|
Or you can use "-border"
(See Adding a Border), using the "-bordercolor" as the color
source.
convert test.png -bordercolor Khaki \
-compose Dst -border 0 color_border.gif
|
|
![[IM Output]](color_border.gif)
|
This last method has the added advantage of also letting you slight enlarge
the image canvas relative to the original images size.
  |
The "-border" method
of generating canvases will not work with versions of IM before version
6.1.4. Before this the background generated by the "-border" operator was not a
simple solid color, but a black canvas surrounded by the border color. Not
very useful.
|
A more flexible (but very slow) method of canvas generation was provided by
the "FX, DIY Operator" operator.
You will also need to use the "+matte" operator to turn off the input images matte channel as by
default "-fx" will not
touch the transparency channel.
convert test.png +matte -fx Gold color_fx_constant.gif
|
|
![[IM Output]](color_fx_constant.gif)
|
The "-fx" operator will even
let you do a little color mathematics.
For example how about a dark gold
color...
convert test.png +matte -fx "Gold*.7" color_fx_math.gif
|
|
![[IM Output]](color_fx_math.gif)
|
All the above methods can not only fill using a fully-opaque color, but can
also use semi-transparent colors. However it is a good idea to ensure the
image you are using has a matte channel using the "
-matte" operator before hand.
Here for example we create a canvas with a semi-transparent red. However when
overlaid on the web pages 'bluish' background we get a off purple color.
convert test.png -matte -fill '#FF000040' -draw 'color 0,0 reset' \
color_semitrans.png
|
|
![[IM Output]](color_semitrans.png)
|
Also for the "
-fx" operator
you will need to set "
-channel" to use all four '
RGBA' color channels.
Other Canvas Techniques
Their lots of other ways of generating canvases of very specific colors, but
they are rather obtuse. As such without some heavy commenting, it may not be
obvious which you are doing when you look at your IM script months or years
later.
I don't recommend these techniques, but are useful to know if you are using
older less flexible versions of IM.
Black Canvas
Traditionally you can create a black canvas by using "-threshold", and then turn off
the matte channel.
convert test.png -threshold 100% +matte black_threshold.png
|
|
![[IM Output]](black_threshold.png)
|
Providing the "-level"
operator with same argument for both 'black' and 'white' points will have the
same effect.
convert test.png -level 100%,100% +matte black_level.png
|
|
![[IM Output]](black_level.png)
|
The "-fx" operator
provides a more obvious way of creating a black canvas by clearing all the
pixels to zero. However you will also need to reset the matte channel to make
it fully opaque.
convert test.png -fx 0 +matte black_fx.png
|
|
![[IM Output]](black_fx.png)
|
However the "-evaluate"
version of this should be faster, particularly on larger images.
convert test.png -evaluate set 0 +matte black_evaluate.png
|
|
![[IM Output]](black_evaluate.png)
|
You can also mis-use the "-gamma" operator to make an image all black.
convert test.png -gamma 0 +matte black_gamma.png
|
|
![[IM Output]](black_gamma.png)
|
A less obvious way is to 'posterize' the image will too few color levels,
resulting in only one color being used, black.
convert test.png -posterize 1 +matte black_posterize.png
|
|
![[IM Output]](black_posterize.png)
|
You can ensure the image is fully transparent then 'extract' the
images mask, using the Alpha Operator
convert test.png -alpha transparent -alpha extract black_alpha.png
| |
![[IM Output]](black_alpha.png)
|
White Canvas
The traditional way is again using "-threshold". The value however must be a negative number, just to
be sure that all colors will be mapped to white, in all versions of IM.
convert test.png -threshold -1 +matte white_threshold.png
|
|
![[IM Output]](white_threshold.png)
|
Providing the "-level"
operator with same argument for both 'black' and 'white' points will have the
same effect.
convert test.png -level -1,-1 +matte white_level.png
|
|
![[IM Output]](white_level.png)
|
You can of course set the pixel values directly using the "-fx" operator.
convert test.png -fx 1.0 +matte white_fx.png
|
|
![[IM Output]](white_fx.png)
|
However the "-evaluate"
version of this should be faster, particularly on larger images.
convert test.png -evaluate set 100% +matte white_evaluate.png
|
|
![[IM Output]](white_evaluate.png)
|
You can also mis-use the "-gamma" operator to make an image all white, by using a negative
argument.
convert test.png -gamma -1 +matte white_gamma.png
|
|
![[IM Output]](white_gamma.png)
|
Or negate some other black canvas generation method.
convert test.png -posterize 1 +matte -negate white_posterize.png
|
|
![[IM Output]](white_posterize.png)
|
You can ensure the image is fully opaque (no transparency) then
'extract' the images mask, using the Alpha Operator
convert test.png -alpha opaque -alpha extract white_alpha.png
| |
![[IM Output]](white_alpha.png)
|
Transparent Canvas
Probably the most important canvas you want to generate from a existing image
is a transparent canvas.
The fastest and easiest way it to just get IM to directly clear the image to
transparency, using the "-alpha transparent" operator (added IM v6.4.3-7).
convert test.png -alpha transparent trans_alpha.png
| |
![[IM Output]](trans_alpha.png)
|
However as this is a very recent addition it is probably not widely available
yet.
We can make a fully-transparent 'black' canvas using the 'Clear alpha composition operator, with any
overlay image (a single pixel "null:" in this case) as it will be
ignored.
convert test.png null: -compose Clear -composite trans_compose.png
| |
![[IM Output]](trans_compose.png)
|
Here we use the "-draw matte" operator to replace the matte
channel value with the tranparency of the "-fill" color setting. In this case
transparent.
convert test.png -fill none -draw 'matte 0,0 reset' color_matte.png
|
|
![[IM Output]](color_matte.png)
|
We can also do this more directly with the "-fx" operator.
convert test.png -channel A -fx 0 trans_fx.png
|
|
![[IM Output]](trans_fx.png)
|
Naturally the "-evaluate" version of this should be faster, particularly on
larger images.
convert test.png -channel A -evaluate set 0 trans_evaluate.png
|
|
![[IM Output]](trans_evaluate.png)
|
Another way to just make the image fully transparent is to use "-threshold" but again
limiting its effects to just the transparency channel.
convert test.png -channel A -threshold -1 trans_threshold.png
|
|
![[IM Output]](trans_threshold.png)
|
Actually in this case we are mathematically dealing with a 'matte' channel,
using threshold to set it to the maximum value, rather than zero, as we did
with the "
-fx" operator.
This is why a '
-1' was used in the above, rather than
100%'. (See
Channels and Masks
examples page.)
The original RGB colors are still present in the last set of images above.
That is the original colors of the image are still present, they have just
been made transparent.
For example, here we read in one of the above images and ask IM to turn off
the matte/alpha channel in the image so as to make the colors visible again.
convert trans_fx.png +matte trans_fx_matte.jpg
|
Note however that not all image formats, and very few image operation will
preserve the not fully-transparent RGB colors that are still present in the
image.
|
![[IM Output]](trans_fx_matte.jpg)
|
As mentioned before, and worth repeating, many of the above methods rely on an
image already having a matte channel. If it doesn't, add one using the
"
-matte" image operator,
or "
-alpha On", but you
may as well just use "
-alpha
Transparent" in that case. See the examples on
Controlling Image Transparency.
Miscellaneous Canvas Coloring
Other than using a specific color, only the "-gamma" operator is truly
flexible enough to generate a canvas of any primary/secondary color. You
basically use 0 to zero out a channel, and -1 to
maximize a channel values.
For example here I generate a yellow canvas...
convert test.png -gamma -1,-1,0 +matte yellow_gamma.png
|
|
![[IM Output]](yellow_gamma.png)
|
As of IM v6.4.2 you can also use the "+level" operator to set a specific grey level for all channels.
convert test.png +level 40%,40% +matte grey_level.png
|
|
![[IM Output]](grey_level.png)
|
Gradients of Color
As you saw above you can create canvases of solid colors easy enough. But
sometimes you want something more interesting. And ImageMagick provides a
large number of special image creation operators that will let you do this.
The full list of these creation operators are listed on the
ImageMagick formats.
It is difficult however to find all the good image generators available in IM
as they are all mixed up with the specific image file formats. And then
not all the options and capabilities are detailed. I will try to rectify
that.
One of the most common image creation operators is gradient. For example...
convert -size 100x100 gradient: gradient.jpg
|
|
![[IM Output]](gradient.jpg)
|
As you can see by default "
gradient:" will create an image with
white at the top, and black at the bottom, and a smooth shading of grey across
the height of the image.
But it does not have to be only a grey-scale gradient, you can also generate
a gradient of different colors by either specifying one color, or both.
convert -size 100x100 gradient:blue gradient_range1.jpg
convert -size 100x100 gradient:yellow gradient_range2.jpg
convert -size 100x100 gradient:green-yellow gradient_range3.jpg
convert -size 100x100 gradient:red-blue gradient_range4.jpg
convert -size 100x100 gradient:tomato-steelblue gradient_range5.jpg
|
![[IM Output]](gradient_range1.jpg)
![[IM Output]](gradient_range2.jpg)
![[IM Output]](gradient_range3.jpg)
![[IM Output]](gradient_range4.jpg)
![[IM Output]](gradient_range5.jpg)
Notice that when given a single color the second color will be either
'
white' or '
black', which ever produces the largest
color distance from the given color. As such '
blue' produces a
'
blue-white' gradient, while '
yellow' generated a
'
yellow-black' gradient.
  |
Gradients can not currently be specified at other angles or involving
more than two colors. However as this ability is in integral part of SVG
gradients, this situation will likely change, with a major improvement in
gradient options.
|
  |
"gradient:" currently does not make use of the "-colorspace" setting.
They are generated only in RGB space, so multi-color 'rainbow' gradients
(using HSV space) are not possible.
|
Some particularly nice gradients include...
convert -size 10x120 gradient:snow-navy gradient_ice-sea.jpg
convert -size 10x120 gradient:gold-firebrick gradient_burnished.jpg
convert -size 10x120 gradient:yellow-limegreen gradient_grassland.jpg
convert -size 10x120 gradient:khaki-tomato gradient_sunset.jpg
convert -size 10x120 gradient:darkcyan-snow gradient_snow_scape.jpg
| |
![[IM Output]](gradient_ice-sea.jpg)
![[IM Output]](gradient_burnished.jpg)
![[IM Output]](gradient_grassland.jpg)
![[IM Output]](gradient_sunset.jpg)
![[IM Output]](gradient_snow_scape.jpg)
|
  |
As of IM v6.3.1 the algorithm used to generate gradients now produce a
perfect gradients, such that all the pixels of each row in an image being
assigned the same color. That is one color per row.
Before this version the "gradient:" operator worked by ignoring
the width of the image, and just assigning the next increment of color,
going row-by-row from top-left corner to the bottom-right of the image.
As a result the gradient was a predominataly vertical gradient, just as it
is now, but not a perfect one. Usually this fact was only important in
special case such as test images, and image Distortion and Displacement Maps.
|
Radial Gradients
As of IM v6.4.4 you can also generate radial gradient images in a simular way.
convert -size 100x100 radial-gradient: rgradient.jpg
|
|
![[IM Output]](rgradient.jpg)
|
Note that the gradient is centered in the middle of the generated image, and
has a diameter set to fit the larger of the X or Y size of the image. So if
the size of the isn't square you will get a 'clipped' radial gradient.
convert -size 100x60 radial-gradient: rgradient_clip.jpg
|
|
![[IM Output]](rgradient_clip.jpg)
|
This lets you easilly generate a square radial gradient from the center to a
corner by making one edge 1.42 (square root of 2) times larger, and crop it.
convert -size 100x142 radial-gradient: \
-gravity center -crop 100x100+0+0 rgradient_crop.jpg
|
|
![[IM Output]](rgradient_crop.jpg)
|
The colors of the gradient itself follow the same conventions as the much
older linear "
gradient:" image
generator.
convert -size 100x100 radial-gradient:blue rgradient_range1.jpg
convert -size 100x100 radial-gradient:yellow rgradient_range2.jpg
convert -size 100x100 radial-gradient:green-yellow rgradient_range3.jpg
convert -size 100x100 radial-gradient:red-blue rgradient_range4.jpg
convert -size 100x100 radial-gradient:tomato-steelblue rgradient_range5.jpg
|
![[IM Output]](rgradient_range1.jpg)
![[IM Output]](rgradient_range2.jpg)
![[IM Output]](rgradient_range3.jpg)
![[IM Output]](rgradient_range4.jpg)
![[IM Output]](rgradient_range5.jpg)
Gradients with Transparency
As of IM v6.2.9-8 the "gradient:" (and later
"radial-gradient:") image creation operator understands the use
of transparent and semi-transparent colors.
convert -size 100x100 gradient:none-firebrick gradient_transparent.png
| |
![[IM Output]](gradient_transparent.png)
|
Of course as I used semi-transparent pixels in this gradient, I needed to use
the PNG image format, rather than JPEG.
One word of warning about such a gradient. It is not a pure color to
transparency, but a mix of that color with "
black". The reason
is that the color "
none" is really transparent-black. The cause
of this problem is the the non-linear nature of RGBA
Color Spaces.
For a proper pure color gradient from opaque to transparency, you can use this
method instead...
convert -size 100x100 gradient:none-black \
-fill firebrick -colorize 100% gradient_pure_trans.png
| |
![[IM Output]](gradient_pure_trans.png)
|
On the other hand you can use this impurity to generate interesting shading
effects. For example by using a transparent-red color instead of
"none", with 'Navy'...
convert -size 100x100 gradient:'rgba(255,0,0,0)-Navy' \
gradient_mixed_trans.png
| |
![[IM Output]](gradient_mixed_trans.png)
|
You can enhance this weirdness by using "-flatten" to then change transparency to some other color,
to make tri-color gradients. Though the middle color will only be half as
intense as the transparency color used.
convert -size 100x100 gradient:'rgba(255,0,0,0)-navy' \
-background yellow -flatten gradient_tricolor.jpg
| |
![[IM Output]](gradient_tricolor.jpg)
|
Gradients by Histogram Adjustment
You can create a non-linear gradient by applying some form of histogram
adjustment to a linear gradient.
For example you can use a
Sigmoidal
Contrast function to create a more natural looking gradient.
convert -size 100x100 gradient: -sigmoidal-contrast 6,50% \
gradient_sigmoidal.jpg
| |
![[IM Output]](gradient_sigmoidal.jpg)
|
This type of gradient is especially good for generating
Overlapping Photos, as it removed the sharp
gradient changes at the beginning of the overlapping region.
Evaluate/Function Gradients
You can also use the
Evaluate Operator
and related
Function Operator
to modify a simple linear gradient.
convert -size 100x100 gradient: -evaluate cos 0.5 -negate \
gradient_cosine.jpg
| |
![[IM Output]](gradient_cosine.jpg)
|
Or take it a step further and make a smooth parabolic peek in the center of
the linear gradient.
convert -size 100x100 gradient: -function Polynomial -4,4,0 \
gradient_peak.jpg
| |
![[IM Output]](gradient_peak.jpg)
|
Or band or a rippled pattern...
convert -size 100x100 gradient: -function sinusoid 4,-90 \
gradient_bands.jpg
| |
![[IM Output]](gradient_bands.jpg)
|
Both of these closely related operators allow you to modfiy images and
gradients basied on Sine Curves, Polynomials, Logithmic and Power-of
mathematical functions.
Distorted Gradients
Rotated Gradient
While the
Sparse Color method '
Barycentric' (see below), provides a
convenient way to generate gradients at any angle, if your IM is older tha
version 6.4.3-0 then you may need to use other methods to generate a diagonal
or rotated gradient.
For example, by increasing the size of the gradient image (multiply by the
square root of 2 or 1.42), then rotate it 45 degrees, and crop the image to
its final size, you can make a diagonal gradient.
convert -size 142x142 gradient: -rotate -45 \
-gravity center -crop 100x100+0+0 +repage \
gradient_diagonal.jpg
| |
![[IM Output]](gradient_diagonal.jpg)
|
As of IM v6.3.5 you have a much faster and simpler way of generating a
rotated gradient by using a
SRT Distortion.
For example, here is a 100 pixel gradient rotated 60 degrees, in a 100x100
pixel image.
convert -size 100x100 gradient: -distort SRT 60 gradient_srt.jpg
| |
![[IM Output]](gradient_srt.jpg)
|
This uses the default
Virtual Pixel, Edge
setting to ensure the whole image is covered by the requested gradient. You
can also use the expert 'distort:viewport' setting, to map a gradient onto a
larger image, such as for a use in
Overlapping
Photos.
Warping Gradients
But you can use the same distortion methods to do a lot more than simple
rotations.
The gradient can also be twisted up...
convert -size 100x100 gradient: -swirl 180 gradient_swirl.jpg
| |
![[IM Output]](gradient_swirl.jpg)
|
You can re-map the gradient into a trapezoidal shape.
convert -size 100x100 gradient: -rotate -90 \
-distort Perspective '0,0 40,0 99,0 59,0 0,99 -10,99 99,99 109,99' \
gradient_trapezoid.jpg
| |
![[IM Output]](gradient_trapezoid.jpg)
|
Or wrap the gradient into a arcs and circles using the
General Distortion Operator...
convert -size 100x100 gradient: -distort Arc '180 0 50 0' \
gradient_arc.jpg
| |
![[IM Output]](gradient_arc.jpg)
|
convert -size 100x100 gradient: -distort Arc '360 0 50 0' \
gradient_circle.jpg
| |
![[IM Output]](gradient_circle.jpg)
|
Though the new "
radial-gradient:"
is probably the more simpler method for generating these gradients.
Even the "
radial-gradient:" can
be warped to produce some interesting non-linear gradients. For example
arcing it using a
Wave Distortion can generate
roughly triangular shaped gradient.
convert -size 100x100 radial-gradient: \
-background black -wave -28x200 -crop 100x100+0+0 +repage \
gradient_triangle.jpg
| |
![[IM Output]](gradient_triangle.jpg)
|
Gradients by Composition
You can also modify gradients by combining them using various composition
methods. For example you can use the
Add
(modulus) compose method to produce venetian blind types of gradients.
convert -size 100x100 gradient: \( +clone +clone \) \
-background gray50 -compose Add -flatten gradient_venetian.jpg
| |
![[IM Output]](gradient_venetian.jpg)
|
And even do this diagonally.
convert -size 100x100 gradient: \( gradient: -rotate -90 \) \
\( -clone 0--1 -clone 0--1 \) \
-background gray50 -compose Add -flatten gradient_vent_diag.jpg
| |
![[IM Output]](gradient_vent_diag.jpg)
|
Or by blending two plain color gradients using either
Channel Copying, or
Mathematical Blending composition methods, you can generate colorful 2
dimensional colormap gradients.
convert -size 100x100 gradient:yellow-blue \
\( gradient:black-lime -rotate -90 \) \
-compose CopyGreen -composite gradient_colormap.jpg
| |
![[IM Output]](gradient_colormap.jpg)
|
Gradients in other Colorspaces
While "
gradient:" generator currently can not generate gradients
directly in some another
Color Spaces,
(only RGB gradients are created) you can transfer gradients into a different
color space to generate interesting effects. For example a linear gradient
copied into the 'Hue' of a '
HSB' image can produce a rainbow
gradient.
convert -size 30x600 xc:'#0F0' -colorspace HSB \
gradient: -compose CopyRed -composite \
-colorspace RGB -rotate 90 gradient_rainbow.jpg
|
![[IM Output]](gradient_rainbow.jpg)
Also see
Combining Channel Images for an
explanation, as well as an example of creating a
Color Wheel image.
Resized Gradient
One trick that was brought up on the
ImageMagick Mailing
List by Glenn Randers-Pehrson, was to create a very small image, two
pixels across, then expand that to the image size needed using "
-resize".
The "
-resize" operator
tries to smooth out enlarged images, to make them look better at the larger
scale. It is this smoothing that we use to generate a non-linear gradient.
For example here we generate the small image using a 'portable bitmap' (or
PBM format) image and feed it into IM for enlargement.
echo "P1 1 2 0 1 " | \
convert - -resize 100x100\! gradient_resize.jpg
|
|
![[IM Output]](gradient_resize.jpg)
|
  |
Some shells like 'csh' and variants, can not handle the '!'
character in the above resize geometry setting very well -- not even in
quotes. Hence the backslash '\' character may be needed.
Caution is advised.
|
The gradient produced is not linear, with a smooth start and finish to the
colors given, making those colors much more pronounced, than you would get
using a normal gradient.
A simple way to generate that initial two pixel image is actually with
gradient itself! This lets you specify the colors directly. Of course that
will limit you to a vertical gradient, unless you rotate the result as well.
convert -size 1x2 gradient:khaki-tomato \
-resize 100x100\! gradient_resize2.jpg
|
|
![[IM Output]](gradient_resize2.jpg)
|
Of course you are not limited to just a single dimension, with this technique.
Here I use a four pixel 'portable greymap' (or PGM image format) to generate a
2-dimensional gradient.
echo "P2 2 2 2 2 1 1 0 " | \
convert - -resize 100x100\! gradient_resize3.jpg
|
|
![[IM Output]](gradient_resize3.jpg)
|
As you can see this diagonal gradient is not very linear when compared to
the rotated diagonal gradient above.
  |
The Network Portable Bitmap
image formats, are very versatile for generating images from scripts.
They can generate bitmaps (P1), greymaps (P2), and pixmaps (P3), in both
ASCII (see above) and binary (P4,P5,P6) formats. Also the quality, or
color range used in each image is completely controllable, allowing you to
use any number range you like to specify the images (see above).
ASIDE: I was the one to make the 1995 release of NetPBM, so I have
experience using this format in script image generators I have created in
the past.
|
The "-resize" operator
smoothes the color between these pixels according to the current "-filter" setting. By adjusting that
parameter (see Resize Filter), you
can make the resize gradient more edge to edge in effect.
convert -size 1x2 gradient: \
-filter Cubic -resize 100x100\! gradient_resize4.jpg
|
|
![[IM Output]](gradient_resize4.jpg)
|
Here is rough "Rainbow Gradient" created using the 'resize' technique.
convert xc:black xc:red xc:yellow xc:green1 xc:cyan xc:blue xc:black \
+append -filter Cubic -resize 600x30\! gradient_rs_rainbow.jpg
|
![[IM Output]](gradient_rs_rainbow.jpg)
Interpolated Lookup Gradients
Another method of generating gradients is to use the special "
-interpolation" setting,
when using a "
-fx" operator.
This setting is used to determine the pixel color returned when the pixel
lookup is not a integer, and thus falls between two or four different pixel
values.
The default setting of '
bilinear' for example will linearly
determine the color for a lookup that falls between two pixels.
convert -size 600x30 xc: \( +size xc:gold xc:firebrick +append \) \
-fx 'v.p{i/(w-1),0}' gradient_interpolated.jpg
|
![[IM Output]](gradient_interpolated.jpg)
Here the lookup X position '
i/(w-1)' goes from '
0.0'
to '
1.0' over the second two pixel image. The floating point
number produces a perfect linear gradient.
Interpolated lookup gradients can also be expanded to 2 dimensions, and
generate square linear gradients, just as easily as purely one dimensions
gradients. Here are examples of the default '
bilinear' "
-interpolate" setting.
convert \( xc:red xc:blue +append \) \( xc:yellow xc:cyan +append \) \
-append -size 100x100 xc: +insert \
-fx 'v.p{i/(w-1),j/(h-1)}' gradient_bilinear.jpg
| |
![[IM Output]](gradient_bilinear.jpg)
|
This same result can also be achieved faster using a '
Triangle'
"
-filter" setting with
the
Resized Gradient technique above.
The '
mesh' "
-interpolate" setting however is not available as a
Resize Filters. It is a special 2 dimensional
interpolation that divides the intra-pixel area into two flat linear
triangles, hinged along the diagonal connecting the corners with the minimal
color difference.
By making the two diagonal corners the same color, you end up with two joined
diagonal gradients.
convert \( xc:red xc:gold +append \) \( xc:gold xc:green +append \) \
-append -size 100x100 xc: +insert -interpolate mesh \
-fx 'v.p{i/(w-1),j/(h-1)}' gradient_mesh.gif
| |
![[IM Output]](gradient_mesh.gif)
|
As the two diagonally opposite yellow corners are the same, a diagonal of
yellow was used to join them. With the other colors linearly mapped to those
triangles.
For more information on the "
-interpolate" setting see
Interpolation Setting.
Roll your own gradient
The
FX DIY Operator, lets you define your own
gradients or other image generation, based on the current pixel position.
As this operator requires an image to work with, you can generate your
gradients or other images to match that image. That is you don't have to know
the size of the image to generate a gradient for it!
For example you can easily generate a linear gradient, sized correctly for
the image you may be working on.
convert rose: -channel G -fx 'i/w' -separate gradient_fx_linear.gif
| |
![[IM Output]](gradient_fx_linear.gif)
|
  |
When generating gray-scale gradients, you can make the -fx operator 3 times
faster, simply by asking it to only generate one color channel only, such as
the 'G' or green channel in the above example. This channel
can then be Separated to form the
required gray-scale image. This can represent a very large speed boost,
especially when using a very complex "-fx" formula.
|
You can even generate some neat non-linear gradients.
convert rose: -channel G -fx '(i/w)^4' -separate gradient_fx_x4.gif
| |
![[IM Output]](gradient_fx_x4.gif)
|
convert rose: -channel G -fx 'cos(pi*(i/w-.5))' \
-separate gradient_fx_cos.gif
| |
![[IM Output]](gradient_fx_cos.gif)
|
How about a 2-dimensional circular radial gradient.
convert -size 100x100 xc: -channel G \
-fx 'rr=hypot(i/w-.5, j/h-.5); 1-rr*1.42' \
-separate gradient_fx_radial.gif
| |
![[IM Output]](gradient_fx_radial.gif)
|
  |
The "-fx" function
'rr=hypot(xx,yy)' was added to IM v6.3.6 to speed up the very
commonly used expression 'rr=sqrt(xx*xx+yy*yy)'. It also meant
that we no longer need to make extra assignments such as
'xx=i/w-.5' when creating a radial gradient.
|
Note how I use some assignment expressions to simplify the calculation of the
distance from center of the image, then convert it to a gradient. This
feature was added in IM v6.3.0.
The value '
1.42' (or
sqrt(2)) in the above controls
the overall size of the gradient relative to the images dimensions. In this
way the radius of the gradient is diagonal distance to the corner.
You can even remove the 'sqrt()' (built into the
'hypot()' function) from the expression to make a more
interesting spherical gradient, which can be useful for 3D Shading Effects.
convert -size 100x100 xc: -channel G \
-fx 'xx=i/w-.5; yy=j/h-.5; rr=xx*xx+yy*yy; 1-rr*4' \
-separate gradient_fx_spherical.gif
| |
![[IM Output]](gradient_fx_spherical.gif)
|
Using a high power function, you can give photos a fade off effect around the
rectangular edges of the image. Adjust the power value '4' to
control the amount of fading.
convert -size 100x100 xc: -channel G \
-fx '(1-(2*i/w-1)^4)*(1-(2*j/h-1)^4)' \
-separate gradient_fx_quad2.gif
| |
![[IM Output]](gradient_fx_quad2.gif)
|
Here is a angular gradient, which is interesting in itself.
convert -size 100x100 xc: -channel G \
-fx '.5 - atan2(j-h/2,w/2-i)/pi/2' \
-separate gradient_fx_angular.gif
| |
![[IM Output]](gradient_fx_angular.gif)
|
Note that the '
atan2(y,x)' function returns a angle in radians
from -PI to +PI (see its manpage), so its output needs to be be scaled and
translated to correctly fit a 0.0 to 1.0 color range. This is why the above
looks so much more complex than it really is.
This last example can be generated faster by
Distorting a Gradient using the
Generalized Distortion Operator. For an example see the
Color Wheel Example.
More Complex DIY Gradients
Of course an FX function can generate color gradients. For example here is a
gradient based on distance ratios, using an extremely complex FX expression.
convert -size 100x100 xc: +size xc:red xc:yellow \
-fx 'ar=hypot( i/w-.8, j/h-.3 )*4;
br=hypot( i/w-.3, j/h-.7 )*4;
u[1]*br/(ar+br) + u[2]*ar/(ar+br)' \
gradient_dist_ratio.gif
| |
![[IM Output]](gradient_dist_ratio.gif)
|
When going from two points to three points the ratio of how much color each
'control point' provides, is a bit more complex, and uses a technique called
Inverse Distance Weighted (IDW) Interpolation. You can see more details math
for this in
Wikipedia, IDW
Here is a inverse distance example for three points.
convert -size 100x100 xc: +size xc:red xc:yellow xc:lime \
-fx 'ar=1/max(1, hypot(i-50,j-10) );
br=1/max(1, hypot(i-10,j-70) );
cr=1/max(1, hypot(i-90,j-90) );
( u[1]*ar + u[2]*br + u[3]*cr )/( ar+br+cr )' \
gradient_shepards.gif
| |
![[IM Output]](gradient_shepards.gif)
|
And here I use a inverse distance squared which is the more normal method used
for a IDW interpolation. This is also known as Shepard's Interpolation method,
and is now implements using the
Sparse Color
method '
Shepards", (see below).
convert -size 100x100 xc: +size xc:red xc:yellow xc:lime \
-fx 'ar=1/max(1, (i-50)*(i-50)+(j-10)*(j-10) );
br=1/max(1, (i-10)*(i-10)+(j-70)*(j-70) );
cr=1/max(1, (i-90)*(i-90)+(j-90)*(j-90) );
( u[1]*ar + u[2]*br + u[3]*cr )/( ar+br+cr )' \
gradient_shepards_2.gif
| |
![[IM Output]](gradient_shepards_2.gif)
|
Note that the '
hypot()' function was not used in the above
as there is no need to generate a square root of the distance.
The problem with Shepard's Method is that all the 'control points' has a
global effect over the whole image. As a result you get a sort of underlying
'average color' in between all the 'control points', and especially at a large
distance from all control points. This, in turn, produces 'spots' of color
rather than a smooth gradient that was wanted.
Here I tried to improve the results by generating the gradient in HSL
colorspace, but this time using blue instead of yellow.
convert -size 100x100 xc: +size xc:red xc:blue xc:lime -colorspace HSL \
-fx 'ar=1/max(1, (i-50)*(i-50)+(j-10)*(j-10) );
br=1/max(1, (i-10)*(i-10)+(j-70)*(j-70) );
cr=1/max(1, (i-90)*(i-90)+(j-90)*(j-90) );
( u[1]*ar + u[2]*br + u[3]*cr )/( ar+br+cr )' \
-colorspace RGB gradient_shepards_HSL.gif
| |
![[IM Output]](gradient_shepards_HSL.gif)
|
As you can see all the colors were nice an bright as we are only generating a
hue gradient. However it also appears very strange, which is caused by the
'cyclic' nature of the 'Hue' color channel. As a consequence the area between
the blue and the red goes the long way round though a green hue, rather than
though a purple hue, as you would expect.
This has no easy solution due to the modulus mathematics that is involved, but
if you have ideas I would welcome them.
Sparse Points of Color
The "
-sparse-color" operator was added to IM v6.4.3-0 will take an
image as set the color given at each of the given floating point
'
x,y' coordinates. That is of the form...
-sparse-color {method} 'x,y color x,y color x,y color ...'
The rest of the pixels in the image will then be mapped to try match those
points of color, according to the method chosen.
Naturally there are lots of ways to define what the intervening color should
be, and which method you choose really depends on what you are attempting to
achieve.
Note that image enlargement (resize magnify) is actually a specialized sub-set
of this, but one where you start with a fixed grid of pixels to be enlarged.
Unfortunately few of the
Resize Filter
Methods will translate well to a free form set of sparsely separated
points of color.
This is also related to "Geographical Information System" methods where
landscapes are measured using sparsely separated points of height (not always
in a strict grid), and the rest of the landscape needs to be determined from
those points.
Voronoi (nearest color)
The "
Voronoi" method, just maps each pixel to the closest
color point you have provided. This basically divides the image into a set of
polygonal 'cells' around each point. For example..
convert -size 100x100 xc: -sparse-color Voronoi \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_voronoi.gif
| |
![[IM Output]](sparse_voronoi.gif)
|
As you can see no attempt is made to provide anti-aliasing of the colored
'cells' around each point. The edge of each cell actually falls exactly
midway between each point's nearest neighbours.
This can be used for example to generate masks to cut up the image in various
ways. just assign one point as white and all the rest as black to extract one
single 'cell' from the image.
If you want to smooth (anti-alias) the result you can either use some form of
Super Sampling to smooth the
image. For example generate one 4 times as big, and "
-scale" it back to the desired
size.
convert -size 400x400 xc: -sparse-color Voronoi \
'120,40 red 40,320 blue 270,240 lime 320,80 yellow' \
-scale 25% -fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_voronoi_ssampled.png
| |
![[IM Output]](sparse_voronoi_ssampled.png)
|
The simpler way (though not very nice) is to just simply blur the image very
slightly...
convert -size 100x100 xc: -sparse-color Voronoi \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-blur 0x1 -fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_voronoi_smoothed.png
| |
![[IM Output]](sparse_voronoi_smoothed.png)
|
By blurring generated image by a large amount you can set up some non-linear
gradients between the 'cells' that was generated.
convert -size 100x100 xc: -sparse-color Voronoi \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-blur 0x15 -fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_voronoi_blur.png
| |
![[IM Output]](sparse_voronoi_blur.png)
|
The larger the "
-blur" the
larger the gradient between the various 'cells'. However be warned that this
may not preserve small colored cells, or ensure the original point remains the
color that was given, if it is close to the edge (and another point) of a
different color.
By using a special 'linear blur' technique developed br Fred Weinhaus, you can
produce a fixed width linear gradient between the cells.
convert -size 100x100 xc: -sparse-color Voronoi \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-blur 10x65535 -fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_voronoi_gradient.png
| |
![[IM Output]](sparse_voronoi_gradient.png)
|
The unblurred output could also passed to various
Edge Detection techniques to generate various bounded edges.
You can remap the image via a
Raster to
Vector Convertor to generate vector lines. However I found the default
'
autotrace' settings may need to be adjusted with
"
-corner-threshold 120" so it will detect the corners better.
Shepards (spots of color)
The "
Shepards" method uses a ratio of the inverse squares of the
distances to each of the given points to determine the color of the canvas at
each point. See
More Complex DIY Gradients
above for examples of how the the mathematics is performed.
It is a bit like having spot lights of color at each point which interacts
with each other, as the light spreads out to a uniform average of all the
given colors at infinity.
convert -size 100x100 xc: -sparse-color Shepards \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_shepards.png
| |
![[IM Output]](sparse_shepards.png)
|
By surrounding a specific area with a similar color you can generate a plateau
of that specific color, though the boundaries between the edging points may
'leak'.
This method is also used to generate a displacement field used in
Shepards Image Distortions. In that case X
and Y vectors are mapped rather than color values.
Channel and Sparse Color
The "
-sparse-color"
operator is effected by the "
-channel" setting which means you can use that setting to limit its
effects to just a single channel, or expand it to the transparency channel.
You can also use the "
-channel" setting to speed up processing of gray-scale images by
only operating on one channel, then "
-separate" that channel (see
Channel Handling for more detail). For
example..
convert -size 100x100 xc: -channel G -sparse-color Shepards \
'30,10 gray70 10,80 black 70,60 white 80,20 gray(33.3333%)' \
-separate +channel -fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_shepards_gray.gif
| |
![[IM Output]](sparse_shepards_gray.gif)
|
Bilinear (4 point gradient)
This method fits an equation to 4 points, over all three color channels to
produce a uniform color gradient between the points, and beyond.
convert -size 100x100 xc: -sparse-color Bilinear \
'30,10 red 10,80 blue 70,60 lime 80,20 yellow' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82' \
-draw 'circle 70,60 70,62 circle 80,20 80,22' \
sparse_bilinear.png
| |
![[IM Output]](sparse_bilinear.png)
|
You can see this 4 point fit by taking the above image and seperating out the
individual color channel gradients.
convert sparse_bilinear.png -separate sparse_bilin_%d.gif
|
![[IM Output]](sparse_bilinear.png)
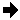
![[IM Output]](sparse_bilin_0.gif)
![[IM Output]](sparse_bilin_1.gif)
![[IM Output]](sparse_bilin_2.gif)
Note how the equation produces curves (quadratic curves actually). However if
the 4 points form parrell lines, the gradient generated will become linear.
This method is actually equivalent to the default
Bilinear Interpolation method (see
Interpolated Lookup Gradients below), when the 4 points are aligned to a
orthogonal (rectangular) grid.
If less than 4 points are given the above function will be replaced by a 3
point '
Barycentric' method (see
below). If more than four points are given it will do a best fit of all the
points, so this is not a good general method for more than 4 point gradients.
Summery of 4 point methods
Here is a repeat of the various, 4 point "
-sparse-color" images, for
comparison.
![[IM Output]](sparse_voronoi.gif)
Voronoi
|
![[IM Output]](sparse_voronoi_blur.png)
Voronoi (blur)
|
![[IM Output]](sparse_shepards.png)
Shepards
|
![[IM Output]](sparse_bilinear.png)
Bilinear
|
Barycentric (triangle gradient)
The "
Barycentric" method, will map three points into a linear
triangle of color. The colors outside this triangle continue as before. I
have again marked the points to make this continuation clear.
convert -size 100x100 xc: -sparse-color Barycentric \
'30,10 red 10,80 blue 70,60 lime' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82 circle 70,60 70,62' \
sparse_barycentric.png
| |
![[IM Output]](sparse_barycentric.png)
|
If more than four points are given a 'best fit' will be performed, over all
the points given, and as such you may not get the exact color specified at the
points you give.
The '
barycentric' method is in reality a mapping of a linear
affine equation to each of the three color channels separately.
As such if I separate each of the color channels of the above three point
example, you get three simple linear gradients in each color channel.
convert sparse_barycentric.png -separate sparse_bary_%d.gif
|
![[IM Output]](sparse_barycentric.png)
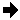
![[IM Output]](sparse_bary_0.gif)
![[IM Output]](sparse_bary_1.gif)
![[IM Output]](sparse_bary_2.gif)
It is only because of the use of primary colors that the above gradients all
were mapped parallel to one of the edges of the triangle. That is not
typically the case.
It does however demonstrate how you can use one point that is the same color
as another point to define the 'angle' of the gradient between the two
original points. For example by making two of the points '
red'
the gradient will be made parallel to the two '
red' points...
convert -size 100x100 xc: -sparse-color Barycentric \
'30,10 red 10,80 red 70,60 lime' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 10,80 10,82 circle 70,60 70,62' \
sparse_bary_gradient.png
| |
![[IM Output]](sparse_bary_gradient.png)
|
If only two color points are given, IM will generate the third point
perpendicular to one of the given points so as to generate a simple linear
gradient between the two original points.
convert -size 100x100 xc: -sparse-color Barycentric \
'30,10 red 70,60 lime' \
-fill white -stroke black \
-draw 'circle 30,10 30,12 circle 70,60 70,62' \
sparse_bary_two_point.png
| |
![[IM Output]](sparse_bary_two_point.png)
|
This provides a simple way of generating a diagonal gradient.
However be warned that the gradient does not just 'stop' but continues to
change beyond those points. Traditionally a barycentric gradient will be
limited to within the enveloping triangle of points used to generate it.
For example..
convert -size 100x100 xc: \
-sparse-color Barycentric '30,5 red 5,80 blue 95,95 lime' \
\( -size 100x100 xc:black -fill white \
-draw 'polygon 30,5 5,80 95,95' \) \
+matte -compose CopyOpacity -composite \
-fill white -stroke black \
-draw 'circle 30,5 30,7 circle 5,80 5,82 circle 95,95 95,97' \
sparse_bary_triangle.png
| |
![[IM Output]](sparse_bary_triangle.png)
|
FUTURE: when a "Triangular Mesh" method is added in the future then you
will get this type of result for the 'mesh' of points given.
More "-sparse-color" methods are planned. If you have any ideas
mail them to me.
Randomized Canvases
Plasma Gradients
While gradients provide a smooth range of colors, another image creation
operator "
plasma:" provides a different sort of gradient. One
that is ideally suited to generating a random backdrop of color for your
images.
First of all I should point out that "
plasma:" is a randomized
image. As such it can and will produce a different image every time it is run.
For example here we generate three separate 'standard' plasma images, and each
image is different from each other, even though the same command was used to
generate them.
convert -size 100x100 plasma: plasma1.jpg
convert -size 100x100 plasma: plasma2.jpg
convert -size 100x100 plasma: plasma3.jpg
|
![[IM Output]](plasma1.jpg)
![[IM Output]](plasma2.jpg)
![[IM Output]](plasma3.jpg)
You can also see that plasma images are also a type of randomized gradient
of colors, and like "
gradient:" started with white at the top and
black at the bottom.
What isn't well document is that you can specify color for the plasma gradient
in the exact same way as you can for linear gradients above.
convert -size 100x100 plasma:blue plasma_range1.jpg
convert -size 100x100 plasma:yellow plasma_range2.jpg
convert -size 100x100 plasma:green-yellow plasma_range3.jpg
convert -size 100x100 plasma:red-blue plasma_range4.jpg
convert -size 100x100 plasma:tomato-steelblue plasma_range5.jpg
|
![[IM Output]](plasma_range1.jpg)
![[IM Output]](plasma_range2.jpg)
![[IM Output]](plasma_range3.jpg)
![[IM Output]](plasma_range4.jpg)
![[IM Output]](plasma_range5.jpg)
You can also see that mid-tone colors like '
tomato' and
'
steelblue' tend to work better than pure colors like
'
red' and '
blue'. That is because it contains at
least some colors from all three color channels, allowing the plasma image
operator more scope in the colors generated.
By using the same color twice with plasma you can produce a background that is
predominantly that color, but with random splotches of colors close to those
of the original colors.
convert -size 100x100 plasma:black-black plasma_black.jpg
convert -size 100x100 plasma:grey-grey plasma_grey.jpg
convert -size 100x100 plasma:white-white plasma_white.jpg
convert -size 100x100 plasma:yellow-yellow plasma_yellow.jpg
convert -size 100x100 plasma:tomato-tomato plasma_tomato.jpg
convert -size 100x100 plasma:steelblue-steelblue plasma_steelblue.jpg
|
![[IM Output]](plasma_black.jpg)
![[IM Output]](plasma_grey.jpg)
![[IM Output]](plasma_white.jpg)
![[IM Output]](plasma_yellow.jpg)
![[IM Output]](plasma_tomato.jpg)
![[IM Output]](plasma_steelblue.jpg)
Again as you can see, mid-tone colors will generate more varieties of color in
the resulting image, than a extreme color, like black, white, or yellow.
The '
grey' plasma in the above is particularly nice giving a
iridescent 'mother-of-pearl' like effect, basically as grey has total freedom
in the colors that the "
plasma:" will generate.
Normalizing a prefect 50% grey plasma will produce a particularly uniform
multi-color plasma image, over the full range of colors, including white and
black.
convert -size 100x100 plasma:grey50-grey50 -normalize plasma_grey_norm.jpg
| |
![[IM Output]](plasma_grey_norm.jpg)
|
Alternatively you can just spread the contrast of the colors to just make
them bolder, but without going to extremes.
convert -size 100x100 plasma:grey50-grey50 \
-sigmoidal-contrast 8x50% plasma_grey_contrast.jpg
| |
![[IM Output]](plasma_grey_contrast.jpg)
|
Compare this image with the 'fractal plasma' images below.
Fractal Plasma
The plasma generator also has a special fractal mode, producing highly
colorful effects. The color generated are enhanced to produce more
exaggerated color changes.
convert -size 100x100 plasma:fractal plasma_fractal1.jpg
convert -size 100x100 plasma:fractal plasma_fractal2.jpg
convert -size 100x100 plasma:fractal plasma_fractal3.jpg
|
![[IM Output]](plasma_fractal1.jpg)
![[IM Output]](plasma_fractal2.jpg)
![[IM Output]](plasma_fractal3.jpg)
In fact this is very similar to the constant color plasma images we have
already seen, and in fact these are generated in the same way but with more
pronounced color changes.
I often find that plasma images are a little 'noisy'. As such they usually
will benefit from a little smoothing using "
-blur".
Here I have have smoothed out the noise from the middle plasma image above.
convert plasma_fractal2.jpg -blur 0x2 plasma_smooth.jpg
| |
![[IM Output]](plasma_smooth.jpg)
|
You can use "-paint" to
create random blotches of color.
convert plasma_fractal2.jpg -blur 0x1 -paint 8 plasma_paint.jpg
| |
![[IM Output]](plasma_paint.jpg)
|
Or make the colors more pronounced and circular using the "-emboss" image operator, after
using "-blur" to remove
the low level noise.
convert plasma_fractal2.jpg -blur 0x5 -emboss 2 plasma_emboss.jpg
| |
![[IM Output]](plasma_emboss.jpg)
|
By using a "-blur"
followed by a "-sharpen" you can produce a more pastel color pattern than we
produced with "-emboss".
convert plasma_fractal2.jpg -blur 0x5 -sharpen 0x15 plasma_sharp.jpg
| |
![[IM Output]](plasma_sharp.jpg)
|
I actually find generating a swirled plasma gradient to be particularly nice,
as a background pattern.
convert -size 160x140 plasma:fractal \
-blur 0x2 -swirl 180 -shave 20x20 plasma_swirl.jpg
| |
![[IM Output]](plasma_swirl.jpg)
|
Greyscale Plasma
Now the plasma generator will always generate color, even on a pure black
solid color. However it is often useful to generate a pure grey-scale plasma.
Well there are two simple ways of doing this.
The simplest way is to take the plasma image and converted it to grey scale.
convert -size 100x100 plasma:fractal -blur 0x2 \
-colorspace Gray plasma_greyscale.jpg
| |
![[IM Output]](plasma_greyscale.jpg)
|
Another way is to copy one of the color channel over the other two, for a
stronger, single layer, effect.
convert -size 100x100 plasma:fractal -blur 0x2 \
-channel G -separate plasma_grey_copy.jpg
| |
![[IM Output]](plasma_grey_copy.jpg)
|
A final technique is to use "-shade" on the plasma.
convert -size 100x100 plasma:fractal -blur 0x5 \
-shade 120x45 -normalize plasma_grey_shade.jpg
| |
![[IM Output]](plasma_grey_shade.jpg)
|
You'd probably think you would get a lot of light and shadow effects, but the
raw plasma is so random, that "
-shade" only seems to produce a more 'mottled plasma' effect.
Instead of using a fractal plasma, with its highly exaggerated color changes,
you can create a grey-scale plasma using the constant color plasma method. As
a side effect, this method also allows you to control the overall brightness
of the grey-scale plasma image generated.
convert -size 100x100 plasma:black-black \
-blur 0x2 -colorspace Gray plasma_grey0.jpg
convert -size 100x100 plasma:grey25-grey25 \
-blur 0x2 -colorspace Gray plasma_grey1.jpg
convert -size 100x100 plasma:grey50-grey50 \
-blur 0x2 -colorspace Gray plasma_grey2.jpg
convert -size 100x100 plasma:grey75-grey75 \
-blur 0x2 -colorspace Gray plasma_grey3.jpg
convert -size 100x100 plasma:white-white \
-blur 0x2 -colorspace Gray plasma_grey4.jpg
|
![[IM Output]](plasma_grey0.jpg)
![[IM Output]](plasma_grey1.jpg)
![[IM Output]](plasma_grey2.jpg)
![[IM Output]](plasma_grey3.jpg)
![[IM Output]](plasma_grey4.jpg)
If this is not quite bold enough, use the channel copy method of grey-scaling
the plasma image.
convert -size 100x100 plasma:black-black \
-blur 0x2 -channel G -separate plasma_grey5.jpg
convert -size 100x100 plasma:grey25-grey25 \
-blur 0x2 -channel G -separate plasma_grey6.jpg
convert -size 100x100 plasma:grey50-grey50 \
-blur 0x2 -channel G -separate plasma_grey7.jpg
convert -size 100x100 plasma:grey75-grey75 \
-blur 0x2 -channel G -separate plasma_grey8.jpg
convert -size 100x100 plasma:white-white \
-blur 0x2 -channel G -separate plasma_grey9.jpg
|
![[IM Output]](plasma_grey5.jpg)
![[IM Output]](plasma_grey6.jpg)
![[IM Output]](plasma_grey7.jpg)
![[IM Output]](plasma_grey8.jpg)
![[IM Output]](plasma_grey9.jpg)
These grey-scale plasma images are very useful for further processing,
allowing you to generate other image effects.
For example, look at the page on
Background
Images for a huge number of examples where the plasma fractal was used
to produce lots of interesting effects.
Seeding or Repeating a Plasma Image
Remember "
plasma:" can produce areas of near pure black or pure
white, or any other color (though it isn't likely to be pure). And while it
is unlikely you will get a image that is all in one color, it is also a
possible outcome. So when you get a good result you may like to save it, for
later re-use.
Because of this, scripts using plasma images, may like to include options to
generate and re-use such randomized images. That is you may like to separate
the plasma image generation from other parts that use that image, to allow
re-use.
A simpler technique however is to 'seed' or initialize the IM random number
generator so that 'plasma:' will generate the same 'randomized'
image. That way you can tune a script or program to produce a good or
interesting coloration or effect, over and over.
convert -size 100x100 -seed 4321 plasma: plasma_seeded.jpg
| |
![[IM Output]](plasma_seeded.jpg)
|
The above image will never change, so unless I change the "
-seed" number I will always have a
'red' area in the bottom-right corner.
Interestingly using the same seed with different initializing color gradients
can produce a set of images which while random, are similar in their internal
pattern.
convert -size 100x100 -seed 4321 plasma:grey-grey plasma_rnd1.jpg
convert -size 100x100 -seed 4321 plasma:white-blue plasma_rnd2.jpg
convert -size 100x100 -seed 4321 plasma:green-yellow plasma_rnd3.jpg
convert -size 100x100 -seed 4321 plasma:red-blue plasma_rnd4.jpg
convert -size 100x100 -seed 4321 plasma:tomato-steelblue plasma_rnd5.jpg
|
![[IM Output]](plasma_rnd1.jpg)
![[IM Output]](plasma_rnd2.jpg)
![[IM Output]](plasma_rnd3.jpg)
![[IM Output]](plasma_rnd4.jpg)
![[IM Output]](plasma_rnd5.jpg)
As you can see the same pattern of colors is present in all the above images,
though the underlying color base can highlight or obscure parts of the
shared pattern.
Just one final word of warning. Other IM operators can also use the random
number generator, such as the "
-fx" '
rand()' function, the "
-virtual-pixel"
'
random' setting the "
-random-threshold"
dither operator, and the "
-noise" operator. As such is a good idea to seed the generator
immediately before your specific use of the random number generator.
As of IM v6.3.4-3, you can also re-randomize the generator using "
+seed". So placing this setting
after your 'seeded plasma' will ensure that any later operators
correctly generate a randomized result if desired.
By default the seed is randomized when IM starts, so you normally do not need
to randomize it yourself using "
+seed" to get a random result.
Problems using Plasma
One problem you should avoid with "
plasma:" images, is generating
them with a high aspect ratio. It tends to distort the normal plasma color
effects, pulling the colors out into needle-like streaks.
convert -size 200x50 plasma: plasma_high_aspect.jpg
|
![[IM Output]](plasma_high_aspect.jpg)
There is no simple solution to this, so unless this is what you are wanting,
caution is advised.
There is also a definite top-left to bottom-right diagonal warp in the plasma
image that should not exist. That is there is some sort of 'spatial bias'
flaw in the algorithm.
For example as Thomas Maus <thomas.maus_AT_alumni.uni-karlsruhe.de>
pointed out if you mirror and append the same plasma image, you will always
see a distinct 'V' in the resulting image...
convert -size 60x60 plasma: \( +clone -flop \) +append plasma_flaw.jpg
|
![[IM Output]](plasma_flaw.jpg)
This should not happen. But the problem seems to be too deep to be able to fix
without basically completely re-writing the whole plasma generator function.
Random Noise Images
As of IM v6.3.5 you can generate a purely random image from an existing image
using Noise Generator, "+noise" method 'Random'.
convert -size 100x100 xc: +noise Random random.png
| |
![[IM Output]](random.png)
|
If your IM is older than this you can still generate a pure random noise image
using the slower DIY FX Operator, "-fx".
convert -size 100x100 xc: -fx 'rand()' random_fx.png
| |
![[IM Output]](random_fx.png)
|
Now these purely random images are themselves not very useful. But as a source
image for various image transformations, they will allow you to generate
a wide variety of different images.
For example by
Blurring the image
and
Color Adjusting the result, you can create
a mottled pattern of random color.
convert random.png -virtual-pixel tile -blur 0x1 -normalize random_1.png
convert random.png -virtual-pixel tile -blur 0x3 -normalize random_3.png
convert random.png -virtual-pixel tile -blur 0x5 -normalize random_5.png
convert random.png -virtual-pixel tile -blur 0x10 -normalize random_10.png
convert random.png -virtual-pixel tile -blur 0x20 -normalize random_20.png
|
![[IM Output]](random.png)
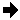
![[IM Output]](random_1.png)
![[IM Output]](random_3.png)
![[IM Output]](random_5.png)
![[IM Output]](random_10.png)
![[IM Output]](random_20.png)
Note however without the
Virtual Pixel
Setting the "
-blur"
operator will have strong edge effects, which are best avoided.
As a bonus by changing the "
-virtual-pixel" setting to '
tile', the randomised
image remains tilable, with the colors wrapping across the image boundaries.
This tiling ability is something that currently not possible with a random
Plasma Images and is a inherent result of pure random
images being so random to start with.
For more methods of processing a random image, and a comparative example for
non-tilable
Plasma Images, see
Generating Backgrounds.
Random Granularity
As you can see from the above you get a image with various blobs of primary
colors. That is because each channel is being processed completely
separately to each other as gray-scale images.
Lets extract one of the channels of each of the above image so you can see the
structure of the blurred image...
convert random.png -channel G -separate random_0_gray.png
convert random_1.png -channel G -separate random_1_gray.png
convert random_3.png -channel G -separate random_3_gray.png
convert random_5.png -channel G -separate random_5_gray.png
convert random_10.png -channel G -separate random_10_gray.png
convert random_20.png -channel G -separate random_20_gray.png
|
![[IM Output]](random_0_gray.png)
![[IM Output]](random_1_gray.png)
![[IM Output]](random_3_gray.png)
![[IM Output]](random_5_gray.png)
![[IM Output]](random_10_gray.png)
![[IM Output]](random_20_gray.png)
The first thing that you should notice is that the image contains equal
amounts of both black and white areas. You can see this if we
Threshold the random images at 50%
convert random_0_gray.png -threshold 50% random_0_thres.png
convert random_1_gray.png -threshold 50% random_1_thres.png
convert random_3_gray.png -threshold 50% random_3_thres.png
convert random_5_gray.png -threshold 50% random_5_thres.png
convert random_10_gray.png -threshold 50% random_10_thres.png
convert random_20_gray.png -threshold 50% random_20_thres.png
|
![[IM Output]](random_0_thres.png)
![[IM Output]](random_1_thres.png)
![[IM Output]](random_3_thres.png)
![[IM Output]](random_5_thres.png)
![[IM Output]](random_10_thres.png)
![[IM Output]](random_20_thres.png)
As you can see you get approximately 50% white and 50% black areas, separated
by a curvy line. Also the curve of this line varies according to the
'
sigma' value used for the blurring of the purely random image. From
individual pixels generating a black and white 'snow' until you get a very
uniform (though still random) separation of the image into two black and white
areas.
Now remember all the above images were generated from the same initial random
image, so they are all related. But every new random image generated will have
a completely different pattern, though the pattern itself will more or less
look rather similar in structure.
The other thing to notice is that you get a sort of interconnected network of
blob like structures, but black and white which are interwoven together.
If instead of thresholding we recolor the image into three equal sets of colors
(using a technique called
Posterization),
you can see that inside each of the black and white zones you get more circle
blobs or 'granules'.
For example here I take the random image blurred with a 'sigma' of 5...
convert random_5_gray.png -ordered-dither threshold,3 random_5_blobs.png
| |
![[IM Output]](random_5_blobs.png)
|
The point at with these individual blobs or 'granules' separate varies from
area to area across the image, but they all average at about a diameter of
about
three times the value used to blur the initial random image.
This '
granularity' (a value of '
5' in that last image) of
the random image is a very important value, as it basically represents the
average size of the circular structures the random image produces. That in
turn is an important factor in much later processing that these images are
used for.
This factor will be used a lot so let me be clear....
The 'Granularity' of a random image (or blur factor)
determines the size of the circular structures within
A '
Granularity' of '
0' will generally produce 'snow' or
'pixel dust' type effects, while successively larger values produce circular
effects with an average diameter of about 3 times that value.
You may also like to try using a 50%
Solarize operation with some extra
Level Adjustments to help simplify the generation of say white
granules on a black background.
For example, here is a full example with a granularity of '8' and
a blob threshold of '15%' generating white spots from both black
and white parts of the image.
convert -size 100x100 xc: +noise random \
-virtual-pixel tile -blur 0x8 -contrast-stretch 0 \
-solarize 50% -threshold 20% \
-negate random_granules.png
| |
![[IM Output]](random_granules.png)
|
Be warned that as the value gets larger, the time to generate the blurred
random image also gets much much longer. Also when the value reaches about
half that of the size of the smallest image dimension, the effect stops
growing as the random image settles into a single white and black spot. Large
values are not recommended.
![[IM Output]](animate_granularity.gif)
To finish with, to the left is showed an animation of varying the
'granularity' (random blurring) of a single random image. The animation was
generated using the shell script "
animate_granularity", which you can download, study and play with.
Note that as the same random image is used as a source the 'granules' or spots
do not really move, but just sort of grow together, or fade away, so as to
produce larger 'granules' with increasing granularity.
Also remember that while I have reduced the number of colors in the animation,
the structure of the full random image is actually smooth gradient between two
sets of white and black granules. This gradient is what makes the image
useful in other techniques.
Random Flux (for animation cycles)
Now as you saw above the granules or spots do not actually move all that much.
But for animation effects you want a pattern that moves in time, but one that
smoothly changes with time. Also you don't want that pattern to just simply
move back and forth, retracing its steps (in a patrol cycle such as the
previous animation example). And finally, you defiantly want that pattern
of movements to repeat, without any sudden jump or jerk as the animation
loops.
So what we need is some way to generate a smoothly repeating pattern. A tall
order. As you need it to be smooth but random, you will need to generate all
the patterns from the same single random image.
Here is an idea that allows you to generate such a random pattern.
Rather than think of each random pixel value as being a random intensity, we
instead think of that value being a 'time' value defining when that point is
at a maximum or minimum intensity. That is we convert that value into a
position on a 'wave' or sine-curve.
Sound complicated, but in reality it isn't. We just multiply the
Random Image using a
Sinusoid Function. Now for each
image in the time sequence we set the time '
phase' for that particular
point in the time cycle.
convert random.png -function Sinusoid 1,{time} \
... do granular blurring, and other processing ...
|
Where time goes from '
0' thru to '
360' over a
complete animation cycle.
The result is that rather than each pixel having a 'static' random value, we
now have one which cycles in a loop between black and white according to time
(or phase). Each pixel will be following this same cycle, but the original
random value will place each pixel at a different (random) point in that
cycle. That is each pixel value cycles over time completely independently to
its neighbours.
For the scientifically minded this is a bit like looking at the 'quantum flux'
that exists at sub-atomic level, where space is far from the 'static' state we
see at normal scales. Hence the name '
Random Flux'.
For example lets generate a time sequence of 6 images...
for i in `seq 0 30 359`; do
convert random.png -channel G -function Sinusoid 1,${i} \
-virtual-pixel tile -blur 0x8 -contrast-stretch 0 \
-separate flux_${i}.png
done
|
And your one random image can now generates a whole sequence images forming a
cycle.
Note that the 'time' extraction has to happen before any other processing such
as blurring, which is probably the slowest part of the whole generation
process.
The other thing to notice is that at phase '
180' (bottom right),
you actually get the exact negative of the first image (top-left). That is
'white' granules has moved to become 'black' granules, and visa-versa. In
fact the whole second half of the animation is actually the negative of the
first half. This can be used to cut down the generation time of a simple
'Random Flux' animation.
Because the image is a negative at a 180 degree phase, you will find that each
'white' granule slowly moves so as to swap places with a neighbouring 'black'
granule. But as the whole second half is a negative of the first the it can't
just simply shuffle back-and-forth, but must either move forward to a new
position, or circle around in a loop, following a circular path.
In other words the white and black granules move in a very non-linear manner.
over the full cycle of the animation.
![[IM Output]](flux_anim.gif)
To the right is an animation of the above frames...
The fluctuating pattern is completely random, but smoothly changing from frame
to frame, and when the animation loops. You can see no beginning or end to
the result. Sometimes you will get a swirling of movement, other times it
looks like all the 'gas' like blobs are being sucked into a dark zone, or just
appearing and fading away again. You also get periods of very fast movements,
as well as very slow movements. It is totally random.
In summery: The same proprieties present in
Blurred
Random Images is also present in this animation. The image remains a
roughly equal division between white and black segments, and it forms blobs of
about
three times the size of the blur or
Granularity of the image. But on top of this you are guarantied that all
parts of the image will form some cycle between both lighter and darker
colors, as half the cycle is the negative of the other half.
One thing you may not have noticed is that due to the conversion of a random
linear value into a sinusoid waveform, you will get a sharper white and black
separation of colors (contrast). As such you may like to use the
de-contrasting aspect of
Sigmoidal Contrast
operator to make the resulting image less 'blob' like, and enhance the
gradient between the granules, rather than the granules themselves.
Now this is only a starting point for what you can do with a cyclic random
animation. Everything that you can do with a
Random
Image, such as described in
Generating Backgrounds, can also be applied to '
Random Flux
Animation'
For example, lets just show the movement of just the 'white' granules...
convert flux_anim.gif -threshold 70% \
-layers Optimize flux_thres_anim.gif
| |
![[IM Output]](flux_thres_anim.gif)
|
Or generate a changing electrical filaments that slowly flow over the image
convert flux_anim.gif \
-sigmoidal-contrast 30x50% -solarize 50% -contrast-stretch 0 \
-set delay 20 -layers Optimize filaments_anim.gif
| |
![[IM Output]](filaments_anim.gif)
|
Note that due to fact that half the cycle is a negation of the first half and
we use a
Solarize to fold the white and
black colors in half, the cycle is actually repeating twice over one animation
cycle. It really needs a lot more frames to remove some of the more sudden
changes that is taking place.
To make the motion less predictable for a longer cyclic sequence, you can also
use some
Gradient Maths to combine
multiple Sinusoidal Cycles, from multiple random images, or even just using
the other color channels of the same random image.
FUTURE: Use the other two randomize color channels to add 'harmonic'
sub-cycles to the original cycle.
Can you come up with a better way of generating a randomized cycle?
Random Specks
Of course you don't have to blur a random image to use it for generating
various effects. For example the individual randomized pixels can be useful
just on their own.
As mentioned previously each of the three
Color Channels of a random image can be thought of as separate random
gray-scale image and these channels can be merged together in various ways.
For example you generate a mask of random dots by first Thresholding a color channel
('G' or the green channel), and separating it out as a gray-scale
image.
convert random.png -channel G -threshold 5% -separate \
+channel -negate random_mask.png
| |
![[IM Output]](random_mask.png)
|
As each color is a linearly random value, the threshold percentage used in the
above directly defines the density of pixels selected.
You can go further and use one color color channel to select random values
from another color channel channel (the '
R' or red channel), by
using various
Image Composition methods.
convert random.png -channel G -threshold 5% -channel RG \
-separate -compose Screen -composite random_white.png
convert random.png -channel G -threshold 5% -negate -channel RG \
-separate -compose Multiply -composite random_black.png
convert random.png -channel G -threshold 5% -negate -channel RG \
-separate -compose CopyOpacity -composite random_trans.png
|
![[IM Output]](random.png)
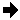
![[IM Output]](random_white.png)
![[IM Output]](random_black.png)
![[IM Output]](random_trans.png)
These type of images are directly usable to generate
Glitter Animations. But with further
processing, particularly on the black background version, will let you enlarge
the dots based on their gray-scale intensity, or generate streaks, and or star
flares, from those dots. For examples see
Star
Generators.
Like
Seeded Plasma Images you can also use the
"
-seed" setting to
pre-initialise the random number generator. This allows you to generate the
same random image(s) repeatably for a particular machine, just as you can for
plasma images.
For more examples of using random images, see
Background Images or to have a look at generating randomised canvases, see
Random Spots of Solid Color.
Tiled Canvases
Tile images can be very large or very small, are designed to fit together
side-by-side and vertically to cover large areas of space.
Thanks to the World Wide Web, there as been an explosion of tile images
available for use (finding what you want is another matter). Below are a set
of tiled images which I copied from
Anthony's Icon Library
for use through out these example pages.
![[IM Output]](bg.gif)
bg.gif
|
![[IM Output]](tile_aqua.jpg)
tile_aqua.jpg
|
![[IM Output]](tile_water.jpg)
tile_water.jpg
|
![[IM Output]](tile_rings.jpg)
tile_rings.jpg
|
![[IM Output]](tile_disks.jpg)
tile_disks.jpg
|
![[IM Output]](tile_weave.gif)
tile_weave.gif
|
Currently there are quite a number of way in which you can tile an image, over
a large area.
You can "
-tile" any image so
as to completely replace the original background image (using the
"
Copy" compose operator). (For more details see
Tile Compositing).
composite -tile tile_weave.gif -size 60x60 xc:none tile_copy.gif
| |
![[IM Output]](tile_copy.gif)
|
Another way is to read in the tile image using "tile:", and
tile it to a specific size.
convert -size 60x60 tile:tile_weave.gif tile_size.gif
| |
![[IM Output]](tile_size.gif)
|
You can use this to generate a tiled image much larger than you need, then use
"
-composite" to overlay
it over the original image. If the tile image is partially transparent then
a '
Over' "
-compose" method will need to be
specified. It is a very slow method of tiling, particularly for large images,
and you have the problem of determining just how big an image you need to
create for the overlay.
convert test.png -size 200x200 tile:tile_disks.jpg \
-composite tile_over.gif
| |
![[IM Output]](tile_over.gif)
|
A more advanced method is to use "
-fx" to tile over an image. This however makes use of a special
"
-virtual-pixel"
setting to define what pixel color to use when a operator references a pixel
outside the boundaries of the actual image. See
Virtual Pixels for details.
convert test.png tile_aqua.jpg -channel RGBA \
-virtual-pixel tile -fx v tile_fx.gif
| |
![[IM Output]](tile_fx.gif)
|
This however is even slower than the previous method. But you can also use
"
-distort" as a faster
method of tiling, with unusual warping options. See
General Distortion Operator.
Finally by specify a tile as 'tile fill pattern' for the "
-draw" operator, you can draw the
tile image over another image, to create any shape or figure you like.
This is because the "
-tile" setting will override any of the "
-fill" color setting used by draw.
See
MVG Drawing Settings.
convert -size 60x60 xc: -tile tile_weave.gif \
-draw "circle 30,30 2,30" tile_draw.gif
| |
![[IM Output]](tile_draw.gif)
|
This only works for "
-draw" and operators like "
-annotate" that also make use
of "
-draw" to perform
their function. It will not work for image operators that use "
-fill" color directly, like
"
label:", "
caption:", and "
text:".
However "-draw" has
built in to it some special color primitives,
such as completely resetting all the pixels in the image to the fill color or
tile pattern (if set).
convert test.png -tile tile_water.jpg -draw "color 0,0 reset" \
tile_test.gif
| |
![[IM Output]](tile_test.gif)
|
This is actually exactly the same method as used by some
Solid Color Canvases methods using a
Specific
Color. Only here we used "
-tile" instead of a "
-fill" color.
Tiling with an Image already In Memory
Tiling an image you have in memory (created or modified) is not straight
forward. Although a few methods are known.
- Using a "Memory Program Register"
- The most straight forward method is to save the the image into a special
'In Memory' file format "
mpr:",
or named 'memory program register'.
From this register you can then either use a "-tile" setting, or use the
special "tile:" image file reader, both of which can only be
set from a 'saved' image file format.
For example using "tile:" to create a tiled image of a
specific size...
convert tree.gif \
-write mpr:tile +delete \
-size 100x100 tile:mpr:tile \
tile_mpr.gif
| |
![[IM Output]](tile_mpr.gif)
|
Or use it to set the "-tile" fill pattern for the various "-draw" operations...
convert tree.gif -write mpr:tile +delete \
granite: -tile mpr:tile -draw 'circle 64,64 10,50' \
tile_mpr_fill.gif
| |
![[IM Output]](tile_mpr_fill.gif)
|
The name given after "mpr:" can
be anything you like, it is only a label on where the image was saved in
memory. It can even be a plain number, color, or source filename.
- Clone/Append In-Memory Tile
- If you are not worried about the exact size of the tiled image, you can
just append the image together multiple times.
For example here we tile the image in a 3x3 array.
convert tree.gif \
\( +clone +clone \) +append \
\( +clone +clone \) -append \
tile_clone.gif
| |
![[IM Output]](tile_clone.gif)
|
This method of tiling has the advantage of allowing you to flip-tile
(mirror tile) the image.
convert tree.gif \
\( +clone -flop +clone \) +append \
\( +clone -flip +clone \) -append \
tile_clone_flip.gif
| |
![[IM Output]](tile_clone_flip.gif)
|
In general this method is only practical when you have some idea of how
big the image being tiled is. Also as clones are actually very fast and
efficient it is a fairly simple and fast tiling method, especially if you
use the results to further tile the larger image.
- Virtual Pixel Tiling
- In this method we use the "
-fx" operator to read a tile image that is 'virtually tiled'.
See Edge Effects and Virtual Pixels
for more details.
This however will junk the tile image and all the other images in memory,
unless you use parenthesis.
convert rose: tree.gif \
-channel RGBA -virtual-pixel tile -fx v \
tile_fx_2.gif
| |
![[IM Output]](tile_fx_2.gif)
|
Note however that using "-fx" to tile images will be a lot slower compared to the
previous methods, though it is probably a little simpler.
You can also use "-distort" to tile images. The size of the final image however
needs to be specified using a special Distort Viewport setting.
convert tree.gif -set option:distort:viewport 100x100+0+0 \
-virtual-pixel tile -distort SRT 0 \
tile_distort.gif
| |
![[IM Output]](tile_distort.gif)
|
By using the General Distortion
Operator in this way, you also have the added bonus of distorting the
tiled image in some very complex ways. For example...
convert tree.gif -set option:distort:viewport 100x100-50-50 \
-virtual-pixel tile -distort Arc '45 0 50' \
tile_distort_polar.gif
| |
![[IM Output]](tile_distort_polar.gif)
|
You can also use the 'mirror'
setting to get the same 'flip-flop' effect of the cloning technique.
Offset Tiling Canvases
Sometimes you need a little more control over the exact positioning of a
background texture, either for aligning a tile pattern with some other image,
or to avoid a bad correlation with some other part of the final image. For
many of the standard tiling methods this can be achieved using the "
-tile-offset" setting.
For example. Here I roll the tile image being used to directly create a tiled
canvas image using "
tile:" or "
pattern:".
convert -size 80x80 -tile-offset +30+30 tile:rose: offset_tile.gif
convert -size 80x80 -tile-offset +20+20 \
pattern:checkerboard offset_pattern.gif
|
![[IM Output]](offset_tile.gif)
![[IM Output]](offset_pattern.gif)
  |
Tile Offset setting was broken before IM
version 6.3.9-9 in that the 'X' offset was being used for both 'X' and 'Y'
offset values (the given 'Y' value was ignored). This means that while the
above examples would have worked (both X and Y offsets are the same) you may
not get the expected results when the two values differ.
|
This also works for the "montage" background
"-texture"
setting.
montage tree.gif -geometry +24+24 \
-tile-offset +30+30 -texture rose: offset_texture.gif
| |
![[IM Output]](offset_texture.gif)
|
You can also use the setting by defining it before the "-tile" or "-fill" setting. For example...
convert -tile-offset +30+30 -tile rose: \
-size 80x80 xc: -draw 'color 30,20 reset' offset_tile_fill.gif
| |
![[IM Output]](offset_tile_fill.gif)
|
However there is one major problem with offset tiling.
The problem is that due to the use of
Legacy
Command Line Style, the above will fail when using built-in
"
pattern:" tiles. For example here I tried the same thing as the
above using a '
checkerboard' tile pattern.
convert -tile-offset +20+20 -tile pattern:checkerboard \
-size 80x80 xc: -draw 'color 30,20 reset' offset_pattern_fail.gif
| |
![[IM Output]](offset_pattern_fail.gif)
|
What is happening is that the first real image processing 'operator' in the
above is '
xc:' and because of this
Legacy Command Line Style reads in all the 'settings' and just applies
them before actually processing the command line in the correct order.
Because of this 'legacy problem' the "
-size" setting gets set BEFORE
the "
-tile" setting
applies the "
pattern:" operator. As a consequence a 80 by 80
pixel 'tile' was generated BEFORE being rolled by the "
-tile-offset" option.
That is turn means the defined "
-tile" setting is a 80x80 pixel tile that will not actually 'tile'
properly. This is because while "
-tile" is regarded a pure setting, internally it calls a image
operator to read the tile, which can make use of the legacy setting handling.
This is probably one of the few examples where this legacy handling is
detrimental to normal IM 'do it as you see it' option handling by IM commands.
The solution to all this is to ensure that the "
-size" setting is reset before
defining the "
-tile"
image, but after any other image has been read in, and thus satisfying IM
legacy option handling.
convert -size 80x80 xc: \
-tile-offset +20+20 +size -tile pattern:checkerboard \
-draw 'color 30,20 reset' offset_pattern_good.gif
| |
![[IM Output]](offset_pattern_good.gif)
|
In any case fact it is probably best to define the tile offset and tile image
just before its first use, which has the same result as the above solution.
Modifying Built-in IM Patterns/Tiles
See the full list of
ImageMagick Built In Images and Patterns. There are a lot of such
patterns, but I'll only look at one or two here.
Now the built-in patterns are generally very very small images, which can tile
to cover large areas. However on their own they are very plain looking, and
rather useless. For example, here is one of the larger more interesting
patterns that is provided...
convert pattern:checkerboard pattern_default.gif
| |
![[IM Output]](pattern_default.gif)
|
Pattern images are usually tiled over an larger areas, either as part of canvas
creation, by setting a "
-size", or as a fill tile (see
Tiled Canvases
above). Without a size setting the default tile size of the pattern will be
used,
30x30 pixels in this case.
Now you will probably notice that all the patterns currently provided by IM
are all pure black and white, with the single exception of the
'
checkerboard' pattern I used in the last example.
Here is one pattern I particularly like to use as a tile pattern...
convert -size 60x60 pattern:hexagons pattern_hexagons.gif
| |
![[IM Output]](pattern_hexagons.gif)
|
If you are not happy with these colors you can replace them using the
"
-opaque" image
operator.
convert -size 60x60 pattern:hexagons \
-fill blue -opaque black -fill skyblue -opaque white \
pattern_colored.gif
| |
![[IM Output]](pattern_colored.gif)
|
If you want color the "
checkerboard" pattern, that is best done
by first using "
-normalize" to map the the two greys to black and white, before
substituting those two colors. Here instead of using "
-opaque" to replace the colors, I
use a "
+level-colors" operator (add IM v6.2.4-1) which is a bit simpler
to use.
convert -size 60x60 pattern:checkerboard -normalize \
+level-colors red,blue pattern_color_checks.gif
| |
![[IM Output]](pattern_color_checks.gif)
|
You can also use "
-floodfill" operator to color the pattern. However for this to
work properly you need to do this,
before you tile the modified
pattern. In this case I also need to expand the tile three times to color it
with the regular pattern of colors I wanted.
convert -size 30x54 pattern:hexagons \
-fill tomato -opaque white \
-fill dodgerblue -draw 'color 10,10 floodfill' \
-fill limegreen -draw 'color 10,25 floodfill' \
-roll +15+27 \
-fill dodgerblue -draw 'color 10,10 floodfill' \
-fill limegreen -draw 'color 10,25 floodfill' miff:- |\
convert -size 100x100 tile:- pattern_color_hexagons.gif
| |
![[IM Output]](pattern_color_hexagons.gif)
|
I used a pipeline of two commands in the above to separate the colored pattern
creation, from its actual usage. If you like to do this with a single command
see
Tiling an Image In Memory above.
You can also warp and distort a simple tiling pattern to produce a interesting
variations. For example a 'wrinkling' effect (technique curtisy of the
wrinkle IM effect from Font Image
Generator) on a hexagon patten I found particularly interesting
convert -size 160x100 pattern:hexagons \
-wave 3x100 -background white -rotate 90 -wave 4x66 -rotate -87 \
-gravity center -crop 120x90+0+0 +repage pattern_distorted.gif
| |
![[IM Output]](pattern_distorted.gif)
|
Modifying Tile Images
The biggest problem people face with modifying tiles, whether it's an existing
tile, or one of the built in patterns, is that many image operations destroy
the 'tilability' of the image.
For example, here I have taken the built-in '
hexagon' pattern, and
tried to modify it to produce a shaded gray-scale pattern of wide hexagonal
lines.
convert pattern:hexagons -rotate 90 \
-blur 0x1 -edge 1 -negate -shade 120x45 \
miff:- |\
convert -size 100x100 tile:- tile_mod_failure.jpg
|
|
![[IM Output]](tile_mod_failure.jpg)
|
As you can see the resulting tile image does NOT tile properly, with
artificial edge distortions clearly visible in the tiled image. Basically we
lost the uniformity of the original tile, along the edges of the image.
One solution is to use a special setting ("
-virtual-pixel") which tells
IM operators to look at the image as a image tile, and wrap the edges around
the image when handling edge colors.
convert pattern:hexagons -rotate 90 -virtual-pixel tile \
-blur 0x1 -edge 1 -negate -shade 120x45 \
miff:- |\
convert -size 100x100 tile:- tile_mod_vpixels.jpg
|
|
![[IM Output]](tile_mod_vpixels.jpg)
|
See
Virtual Pixels, Colors beyond the Image
Bounds for more detail of this setting.
This works for most image operators, especially those using a graphical
technique called
Image Convolving, or color
lookups using the DIY operator "
-fx". Though it does not work for all operators.
For example here we join two related tile patterns together, and use various
effects to create unusual brick wall tile.
convert pattern:leftshingle pattern:rightshingle +append \
-virtual-pixel tile -blur 0x.6 -resize 150% -shade 100x45 \
-fill Peru -tint 100% miff:- |\
convert -size 100x100 tile:- tile_slanted_bricks.jpg
|
|
![[IM Output]](tile_slanted_bricks.jpg)
|
Alternative
There is an alternative to relying on "
-virtual-pixel". This is
especially useful for IM users, using very old versions pre-dating the
addition of this setting.
Basically we provide the 'virtual edge pixels' ourselves, before operating
on the image, so as to avoid any edge effects that may be present. And that
is done by tiling the image over a slightly larger area first. After
modifying the image, we can re-extract the tile, avoiding the edge distortions
that were introduced.
It does not have to be lot bigger, depending on the extent of the image
operations being performed. I have found 15 to 40 pixels should stop all edge
effects in the final result.
To re-extract the image we can either "
-shave" off the extra pixels, or
"
-crop" the original tile
size from the middle of the processed image.
For example here I create a 3d "
-shade" effect using the built-in '
hexagons' pattern.
convert -size 60x60 tile:pattern:hexagons -rotate 90 \
-blur 0x1 -edge 1 -negate -shade 120x45 \
-gravity center -crop 18x30+0+0 +repage miff:- |\
convert -size 100x100 tile:- tile_mod_success.jpg
|
|
![[IM Output]](tile_mod_success.jpg)
|
Note the exact position of the extracted tile does not matter. A tilable
image can be cut anywhere from the tiled image, as long as it is away from the
distorted edges, and use the same original size of the tile.
Here instead of tiling the image over a larger area, we use a 'double clone'
technique to double the area the tile covers. When finished we then just
center crop 50% of the image to recover our modified tile. This means we have
no need to know the exact size of the tile you are processing.
convert pattern:circles \( +clone \) +append \( +clone \) -append \
-fill grey -opaque black -blur 0x0.5 -shade 120x45 \
-gravity center -crop 50% +repage miff:- |\
convert -size 100x100 tile:- tile_circles.jpg
|
|
![[IM Output]](tile_circles.jpg)
|
Generating Tile Images
The biggest problem you face when generating images which can tile together is
trying to match the edges and corners of the image so that they can fit
together seamlessly. If this is not done then all you get is a set of square
boxes each with a repeated copy of the image.
This is not an easy matter and can be a very frustrating and hair pulling
experience. An object appearing in the tile on one edge must re-appear on the
other side of the image in order to re-form the whole when the image is tiled. While
you can do this fairly easily with computer generated images, it is next to
impossible to produce a good tiling image featuring real-world photographs.
The other major problem is trying to make a the tile not look like it is
repeating. The only true solution to this is to make your tile images large
enough to contain enough very similar but still different elements that it
becomes difficult to see a repeated pattern. Because of this generating small
tiles that do not seem to repeat is especially difficult.
FUTURE: Ideas and suggestions for generating tile patterns? Anyone?
Or roll, add element, roll, add element, etc...
Any and all suggestions and examples accepted.
Suggestions for generating tile from real photos of repeating patterns.
Such as water, fallen leaves, clouds, stucco, brickwork, etc...
Generating Escher-like tile patterns.
Random Noise Tile
Because a raw random noise canvas has no edges characteristics to begin with
(every pixel color is completely independent of any of its neighbours), you
can tile it without worry about edge distortions. Basically it is so
extremely random at the pixel level, no edges match to begin with, so we don't
lose anything, by tiling.
Unfortunately very few situations would use a raw random noise image, as is,
for any real purpose. It is just so horribly random that it is useless.
However by modifying the image while preserving its inherent tilability, we
can make just about any randomised tile pattern we want.
For example lets look at the a basic "-blur" of the original tile, using the same 'modifying a tile'
technique we used in the last example.
convert -size 64x64 xc: +noise Random -write mpr:rand \
-virtual-pixel tile -blur 0x6 -normalize tile_random.jpg
convert -size 128x128 tile:tile_random.jpg tiled_random.jpg
|
|
![[IM Output]](tile_random.jpg)
![[IM Output]](tiled_random.jpg)
|
Using this technique you can apply just about any transformation to a raw
random noise image image. For example...
convert -size 64x64 xc: +noise Random -write mpr:rand \
-virtual-pixel tile -blur 0x6 -edge 1 -fx G \
-shade 280x45 -normalize tile_random_pits.jpg
convert -size 128x128 tile:tile_random_pits.jpg tiled_random_pits.jpg
|
|
![[IM Output]](tile_random_pits.jpg)
![[IM Output]](tiled_random_pits.jpg)
|
As you can see it is a lot simpler to create randomized tiles using the raw
random noise image, and you will not have any edge distortions in the results.
This particular image transformation is listed on the
Background Images page and is titles "pits". See
that page for lots of other image transformations, and examples of what they
look like.
Hexagonal Tiling
Rather than tile in a square fashion, the 'random noise' image allows use to
generate a very different sort of tile. By doubling the image dimensions
and re-laying the tile in the extra space, but offset by half, we can generate
a basic random noise hexagonal tile pattern.
This is the same sort of tiling effect we get when we tile the special
"pattern:hexagons" built-in of ImageMagick.
convert pattern:hexagons tile_hexagons.gif
convert -size 64x64 pattern:hexagons tiled_hexagons.gif
|
|
![[IM Output]](tile_hexagons.gif)
![[IM Output]](tiled_hexagons.gif)
|
Note however that for this tile to look 'hexagonal' the tile can not be a
normal square, or even a doubled square. The final tile size needs to be a
rectangle somewhere in between. A good ratio is 4:3, as this is usually the
ratio used by most computer and digital camera images.
Here we overlay the same 'random noise' image (with a 2:3 ratio) three times
to generate the basic hex pattern, double the width of that in pre-mapped
image (producing a final 4:3 ratio tile image).
The hexagonal random noise tile is then transformed using the "paint_3s"
transformation from the Background Images page.
convert -size 48x64 xc: +noise Random -write mpr:rand \
-extent 96x64 -page +48-32 mpr:rand -page +48+32 mpr:rand \
-flatten tile_hex_random.jpg
convert tile_hex_random.jpg -virtual-pixel tile -blur 0x10 -paint 3 \
-shade 280x45 -normalize tile_hex_layered.jpg
convert -size 160x160 tile:tile_hex_layered.jpg tiled_hex_layered.jpg
|
|
![[IM Output]](tile_hex_layered.jpg)
![[IM Output]](tiled_hex_layered.jpg)
|
If you look at the pattern the tile produces you will see that any specific
feature, will have 6 copies of that same feature surrounding it in a circle.
This is the 'hexagonal' pattern the tile produces, even though it is still
tiled in the same 'square' pattern as all other tiling images.
One variant of the above 'hextile' pattern is to double up the tile image
vertically, rather than horizontally as we have done above. The result is
that the hexagonal pattern will be rotated ninety degrees, but is still the
same type of pattern.
Triple Hex Tiling
Like we did with the "
hexagons" built-in pattern, you can make
three variants to of the initial tile, (typically rotations) before re-mapping
them to form the larger tile.
The problem, is that the final tile image will need to be enlarged three times
more than what we'd get with a normal 'hexagonal tiling pattern.
The variations between the three tiles generated must not be too different,
and should survive any post-processing, otherwise you will not get the benefits
of the technique. This means the initial tile must be reasonably large as
well, so any distinct features present will be preserved.
For example here we take a very simple line drawing, and rotate it to produce
3 similar variations. These rotated images are then tiled seven times onto a
larger canvas (6 times larger) to produce the triple image hex pattern.
convert -size 24x24 xc: -draw "rectangle 3,11 20,12" tile_line.gif
convert tile_line.gif -gravity center\
\( +clone -rotate 0 -crop 24x18+0+0 -write mpr:r1 +delete \) \
\( +clone -rotate 120 -crop 24x18+0+0 -write mpr:r2 +delete \) \
-rotate -120 -crop 24x18+0+0 -write mpr:r3 +repage \
-extent 72x36 -page +0+0 mpr:r3 \
-page +24+0 mpr:r1 -page +48+0 mpr:r2 \
-page -12+18 mpr:r1 -page +12+18 mpr:r2 \
-page +36+18 mpr:r3 -page +60+18 mpr:r1 \
-flatten tile_hex_lines.jpg
convert -size 120x120 tile:tile_hex_lines.jpg tiled_hex_lines.jpg
|
|
![[IM Output]](tile_line.gif)
![[IM Output]](tile_hex_lines.jpg)
![[IM Output]](tiled_hex_lines.jpg)
|
The above however only works for tiling a small shape in the middle of the
original image. It does not work well for a general image.
For a general image hex tiling we also need to rotate and mask out an
equilateral triangle the pieces of when then needs to be put together again.
This is not easy.
A German artist, Günter Bachelier, (see his web page
Trance Art) has
endeavored to work out the mathematics of this tiling procedure, for very high
resolution images. See his draft document
p3m1_tile (PDF). This is part of a larger work of art that were evolved
via the use of computers.
Also see his work on another tiling scheme,
p6m_e (PDF).
![[IM Output]](canvas_khaki.gif)
![[IM Output]](canvas_opaque.gif)
![[IM Output]](canvas_pick.gif)
![[IM Output]](test.png)
![[IM Output]](color_colorize.gif)
![[IM Output]](color_levelc.gif)
![[IM Output]](color_sparse.gif)
![[IM Output]](color_reset.gif)
![[IM Output]](color_flatten.gif)
![[IM Output]](color_extent.gif)
![[IM Output]](color_border.gif)
![[IM Output]](color_fx_constant.gif)
![[IM Output]](color_fx_math.gif)
![[IM Output]](black_threshold.png)
![[IM Output]](black_level.png)
![[IM Output]](black_fx.png)
![[IM Output]](black_evaluate.png)
![[IM Output]](black_gamma.png)
![[IM Output]](black_posterize.png)
![[IM Output]](black_alpha.png)
![[IM Output]](white_threshold.png)
![[IM Output]](white_level.png)
![[IM Output]](white_fx.png)
![[IM Output]](white_evaluate.png)
![[IM Output]](white_gamma.png)
![[IM Output]](white_posterize.png)
![[IM Output]](white_alpha.png)
![[IM Output]](trans_alpha.png)
![[IM Output]](trans_compose.png)
![[IM Output]](color_matte.png)
![[IM Output]](trans_fx.png)
![[IM Output]](trans_evaluate.png)
![[IM Output]](trans_threshold.png)
![[IM Output]](trans_fx_matte.jpg)
![[IM Output]](yellow_gamma.png)
![[IM Output]](grey_level.png)
![[IM Output]](gradient.jpg)
![[IM Output]](gradient_range1.jpg)
![[IM Output]](gradient_range2.jpg)
![[IM Output]](gradient_range3.jpg)
![[IM Output]](gradient_range4.jpg)
![[IM Output]](gradient_range5.jpg)
![[IM Output]](rgradient.jpg)
![[IM Output]](rgradient_clip.jpg)
![[IM Output]](rgradient_crop.jpg)
![[IM Output]](rgradient_range1.jpg)
![[IM Output]](rgradient_range2.jpg)
![[IM Output]](rgradient_range3.jpg)
![[IM Output]](rgradient_range4.jpg)
![[IM Output]](rgradient_range5.jpg)
![[IM Output]](gradient_transparent.png)
![[IM Output]](gradient_pure_trans.png)
![[IM Output]](gradient_mixed_trans.png)
![[IM Output]](gradient_tricolor.jpg)
![[IM Output]](gradient_sigmoidal.jpg)
![[IM Output]](gradient_cosine.jpg)
![[IM Output]](gradient_peak.jpg)
![[IM Output]](gradient_bands.jpg)
![[IM Output]](gradient_diagonal.jpg)
![[IM Output]](gradient_srt.jpg)
![[IM Output]](gradient_swirl.jpg)
![[IM Output]](gradient_trapezoid.jpg)
![[IM Output]](gradient_arc.jpg)
![[IM Output]](gradient_circle.jpg)
![[IM Output]](gradient_triangle.jpg)
![[IM Output]](gradient_venetian.jpg)
![[IM Output]](gradient_vent_diag.jpg)
![[IM Output]](gradient_colormap.jpg)
![[IM Output]](gradient_resize.jpg)
![[IM Output]](gradient_resize2.jpg)
![[IM Output]](gradient_resize3.jpg)
![[IM Output]](gradient_resize4.jpg)
![[IM Output]](gradient_bilinear.jpg)
![[IM Output]](gradient_mesh.gif)
![[IM Output]](gradient_fx_linear.gif)
![[IM Output]](gradient_fx_x4.gif)
![[IM Output]](gradient_fx_cos.gif)
![[IM Output]](gradient_fx_radial.gif)
![[IM Output]](gradient_fx_spherical.gif)
![[IM Output]](gradient_fx_quad2.gif)
![[IM Output]](gradient_fx_angular.gif)
![[IM Output]](gradient_dist_ratio.gif)
![[IM Output]](gradient_shepards.gif)
![[IM Output]](gradient_shepards_2.gif)
![[IM Output]](gradient_shepards_HSL.gif)
![[IM Output]](sparse_voronoi.gif)
![[IM Output]](sparse_voronoi_ssampled.png)
![[IM Output]](sparse_voronoi_smoothed.png)
![[IM Output]](sparse_voronoi_blur.png)
![[IM Output]](sparse_voronoi_gradient.png)
![[IM Output]](sparse_shepards.png)
![[IM Output]](sparse_shepards_gray.gif)
![[IM Output]](sparse_bilinear.png)
![[IM Output]](sparse_voronoi.gif)
![[IM Output]](sparse_voronoi_blur.png)
![[IM Output]](sparse_shepards.png)
![[IM Output]](sparse_bilinear.png)
![[IM Output]](sparse_barycentric.png)
![[IM Output]](sparse_bary_gradient.png)
![[IM Output]](sparse_bary_two_point.png)
![[IM Output]](sparse_bary_triangle.png)
![[IM Output]](plasma1.jpg)
![[IM Output]](plasma2.jpg)
![[IM Output]](plasma3.jpg)
![[IM Output]](plasma_range1.jpg)
![[IM Output]](plasma_range2.jpg)
![[IM Output]](plasma_range3.jpg)
![[IM Output]](plasma_range4.jpg)
![[IM Output]](plasma_range5.jpg)
![[IM Output]](plasma_black.jpg)
![[IM Output]](plasma_grey.jpg)
![[IM Output]](plasma_white.jpg)
![[IM Output]](plasma_yellow.jpg)
![[IM Output]](plasma_tomato.jpg)
![[IM Output]](plasma_steelblue.jpg)
![[IM Output]](plasma_grey_norm.jpg)
![[IM Output]](plasma_grey_contrast.jpg)
![[IM Output]](plasma_fractal1.jpg)
![[IM Output]](plasma_fractal2.jpg)
![[IM Output]](plasma_fractal3.jpg)
![[IM Output]](plasma_smooth.jpg)
![[IM Output]](plasma_paint.jpg)
![[IM Output]](plasma_emboss.jpg)
![[IM Output]](plasma_sharp.jpg)
![[IM Output]](plasma_swirl.jpg)
![[IM Output]](plasma_greyscale.jpg)
![[IM Output]](plasma_grey_copy.jpg)
![[IM Output]](plasma_grey_shade.jpg)
![[IM Output]](plasma_grey0.jpg)
![[IM Output]](plasma_grey1.jpg)
![[IM Output]](plasma_grey2.jpg)
![[IM Output]](plasma_grey3.jpg)
![[IM Output]](plasma_grey4.jpg)
![[IM Output]](plasma_grey5.jpg)
![[IM Output]](plasma_grey6.jpg)
![[IM Output]](plasma_grey7.jpg)
![[IM Output]](plasma_grey8.jpg)
![[IM Output]](plasma_grey9.jpg)
![[IM Output]](plasma_seeded.jpg)
![[IM Output]](plasma_rnd1.jpg)
![[IM Output]](plasma_rnd2.jpg)
![[IM Output]](plasma_rnd3.jpg)
![[IM Output]](plasma_rnd4.jpg)
![[IM Output]](plasma_rnd5.jpg)
![[IM Output]](random.png)
![[IM Output]](random_fx.png)
![[IM Output]](random.png)
![[IM Output]](random_1.png)
![[IM Output]](random_3.png)
![[IM Output]](random_5.png)
![[IM Output]](random_10.png)
![[IM Output]](random_20.png)
![[IM Output]](random_0_gray.png)
![[IM Output]](random_1_gray.png)
![[IM Output]](random_3_gray.png)
![[IM Output]](random_5_gray.png)
![[IM Output]](random_10_gray.png)
![[IM Output]](random_20_gray.png)
![[IM Output]](random_0_thres.png)
![[IM Output]](random_1_thres.png)
![[IM Output]](random_3_thres.png)
![[IM Output]](random_5_thres.png)
![[IM Output]](random_10_thres.png)
![[IM Output]](random_20_thres.png)
![[IM Output]](random_5_blobs.png)
![[IM Output]](random_granules.png)
![[IM Output]](animate_granularity.gif) To finish with, to the left is showed an animation of varying the
'granularity' (random blurring) of a single random image. The animation was
generated using the shell script "
To finish with, to the left is showed an animation of varying the
'granularity' (random blurring) of a single random image. The animation was
generated using the shell script "![[IM Output]](flux_0.png)
![[IM Output]](flux_30.png)
![[IM Output]](flux_60.png)
![[IM Output]](flux_90.png)
![[IM Output]](flux_120.png)
![[IM Output]](flux_150.png)
![[IM Output]](flux_330.png)
![[IM Output]](flux_300.png)
![[IM Output]](flux_270.png)
![[IM Output]](flux_240.png)
![[IM Output]](flux_210.png)
![[IM Output]](flux_180.png)
![[IM Output]](flux_anim.gif) To the right is an animation of the above frames...
The fluctuating pattern is completely random, but smoothly changing from frame
to frame, and when the animation loops. You can see no beginning or end to
the result. Sometimes you will get a swirling of movement, other times it
looks like all the 'gas' like blobs are being sucked into a dark zone, or just
appearing and fading away again. You also get periods of very fast movements,
as well as very slow movements. It is totally random.
In summery: The same proprieties present in Blurred
Random Images is also present in this animation. The image remains a
roughly equal division between white and black segments, and it forms blobs of
about three times the size of the blur or Granularity of the image. But on top of this you are guarantied that all
parts of the image will form some cycle between both lighter and darker
colors, as half the cycle is the negative of the other half.
One thing you may not have noticed is that due to the conversion of a random
linear value into a sinusoid waveform, you will get a sharper white and black
separation of colors (contrast). As such you may like to use the
de-contrasting aspect of Sigmoidal Contrast
operator to make the resulting image less 'blob' like, and enhance the
gradient between the granules, rather than the granules themselves.
Now this is only a starting point for what you can do with a cyclic random
animation. Everything that you can do with a Random
Image, such as described in Generating Backgrounds, can also be applied to 'Random Flux
Animation'
To the right is an animation of the above frames...
The fluctuating pattern is completely random, but smoothly changing from frame
to frame, and when the animation loops. You can see no beginning or end to
the result. Sometimes you will get a swirling of movement, other times it
looks like all the 'gas' like blobs are being sucked into a dark zone, or just
appearing and fading away again. You also get periods of very fast movements,
as well as very slow movements. It is totally random.
In summery: The same proprieties present in Blurred
Random Images is also present in this animation. The image remains a
roughly equal division between white and black segments, and it forms blobs of
about three times the size of the blur or Granularity of the image. But on top of this you are guarantied that all
parts of the image will form some cycle between both lighter and darker
colors, as half the cycle is the negative of the other half.
One thing you may not have noticed is that due to the conversion of a random
linear value into a sinusoid waveform, you will get a sharper white and black
separation of colors (contrast). As such you may like to use the
de-contrasting aspect of Sigmoidal Contrast
operator to make the resulting image less 'blob' like, and enhance the
gradient between the granules, rather than the granules themselves.
Now this is only a starting point for what you can do with a cyclic random
animation. Everything that you can do with a Random
Image, such as described in Generating Backgrounds, can also be applied to 'Random Flux
Animation'
![[IM Output]](flux_thres_anim.gif)
![[IM Output]](filaments_anim.gif)
![[IM Output]](random_mask.png)
![[IM Output]](random.png)
![[IM Output]](random_white.png)
![[IM Output]](random_black.png)
![[IM Output]](random_trans.png)
![[IM Output]](bg.gif)
![[IM Output]](tile_aqua.jpg)
![[IM Output]](tile_water.jpg)
![[IM Output]](tile_rings.jpg)
![[IM Output]](tile_disks.jpg)
![[IM Output]](tile_weave.gif)
![[IM Output]](tile_copy.gif)
![[IM Output]](tile_size.gif)
![[IM Output]](tile_over.gif)
![[IM Output]](tile_fx.gif)
![[IM Output]](tile_draw.gif)
![[IM Output]](tile_test.gif)
![[IM Output]](tile_mpr.gif)
![[IM Output]](tile_mpr_fill.gif)
![[IM Output]](tile_clone.gif)
![[IM Output]](tile_clone_flip.gif)
![[IM Output]](tile_distort.gif)
![[IM Output]](tile_distort_polar.gif)
![[IM Output]](offset_tile.gif)
![[IM Output]](offset_pattern.gif)
![[IM Output]](offset_texture.gif)
![[IM Output]](offset_tile_fill.gif)
![[IM Output]](offset_pattern_fail.gif)
![[IM Output]](offset_pattern_good.gif)
![[IM Output]](pattern_hexagons.gif)
![[IM Output]](pattern_colored.gif)
![[IM Output]](pattern_color_checks.gif)
![[IM Output]](pattern_color_hexagons.gif)
![[IM Output]](pattern_distorted.gif)
![[IM Output]](tile_mod_failure.jpg)
![[IM Output]](tile_slanted_bricks.jpg)
![[IM Output]](tile_mod_success.jpg)
![[IM Output]](tile_circles.jpg)
![[IM Output]](tile_random.jpg)
![[IM Output]](tiled_random.jpg)
![[IM Output]](tile_random_pits.jpg)
![[IM Output]](tiled_random_pits.jpg)
![[IM Output]](tiled_hexagons.gif)
![[IM Output]](tile_hex_layered.jpg)
![[IM Output]](tiled_hex_layered.jpg)
![[IM Output]](tiled_hex_lines.jpg)
![[version image]](version.gif)
